第141页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
- 第208页
- 第209页
- 第210页
- 第211页
- 第212页
- 第213页
- 第214页
- 第215页
- 第216页
- 第217页
- 第218页
- 第219页
- 第220页
- 第221页
- 第222页
- 第223页
- 第224页
- 第225页
- 第226页
- 第227页
- 第228页
- 第229页
- 第230页
- 第231页
- 第232页
- 第233页
- 第234页
- 第235页
- 第236页
- 第237页
1.(2024·东莞二模)综合与实践.
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为n°的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽,
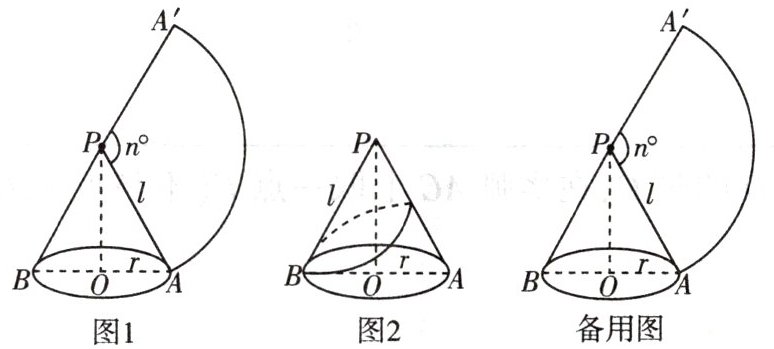
(1)现在需要制作一个r= 10 cm,l= 30 cm的生日帽,请帮忙计算出所需扇形纸板的圆心角度数;
(2)为了使(1)中所制作的生日帽更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),求彩带长度的最小值.
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为n°的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽,

(1)现在需要制作一个r= 10 cm,l= 30 cm的生日帽,请帮忙计算出所需扇形纸板的圆心角度数;
(2)为了使(1)中所制作的生日帽更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),求彩带长度的最小值.
答案:
解:
(1)
∵ $ r = 10 \mathrm { cm } $,$ l = 30 \mathrm { cm } $,
$ \frac { 1 } { 2 } × 2 \pi r × l = \frac { n \pi l ^ { 2 } } { 360 } $.
$ \therefore n = \frac { 360 r } { l } = \frac { 360 × 10 } { 30 } = 120 $
$ \therefore $ 扇形纸板的圆心角度数为 $ 120 ^ { \circ } $;
(2) 如图所示,连接 $ A A ^ { \prime } $,过点 $ P $ 作 $ P H \perp A A ^ { \prime } $,线段 $ A A ^ { \prime } $ 就是彩带长度的最小值,

由
(1) 得 $ P A = P A ^ { \prime } = 30 \mathrm { cm } $,$ \angle A P A ^ { \prime } = 120 ^ { \circ } $,
$ \therefore \angle A P H = \angle A ^ { \prime } P H = 60 ^ { \circ } $,$ A H = A ^ { \prime } H $,
$ \therefore \angle P A ^ { \prime } H = 30 ^ { \circ } $,
$ \therefore P H = \frac { 1 } { 2 } P A = 15 \mathrm { cm } $.
$ \therefore A H = \sqrt { A P ^ { 2 } - P H ^ { 2 } } = 15 \sqrt { 3 } \mathrm { cm } $,
$ \therefore A A ^ { \prime } = 2 A H = 30 \sqrt { 3 } \mathrm { cm } $,
$ \therefore $ 彩带长度的最小值为 $ 30 \sqrt { 3 } \mathrm { cm } $.
解:
(1)
∵ $ r = 10 \mathrm { cm } $,$ l = 30 \mathrm { cm } $,
$ \frac { 1 } { 2 } × 2 \pi r × l = \frac { n \pi l ^ { 2 } } { 360 } $.
$ \therefore n = \frac { 360 r } { l } = \frac { 360 × 10 } { 30 } = 120 $
$ \therefore $ 扇形纸板的圆心角度数为 $ 120 ^ { \circ } $;
(2) 如图所示,连接 $ A A ^ { \prime } $,过点 $ P $ 作 $ P H \perp A A ^ { \prime } $,线段 $ A A ^ { \prime } $ 就是彩带长度的最小值,

由
(1) 得 $ P A = P A ^ { \prime } = 30 \mathrm { cm } $,$ \angle A P A ^ { \prime } = 120 ^ { \circ } $,
$ \therefore \angle A P H = \angle A ^ { \prime } P H = 60 ^ { \circ } $,$ A H = A ^ { \prime } H $,
$ \therefore \angle P A ^ { \prime } H = 30 ^ { \circ } $,
$ \therefore P H = \frac { 1 } { 2 } P A = 15 \mathrm { cm } $.
$ \therefore A H = \sqrt { A P ^ { 2 } - P H ^ { 2 } } = 15 \sqrt { 3 } \mathrm { cm } $,
$ \therefore A A ^ { \prime } = 2 A H = 30 \sqrt { 3 } \mathrm { cm } $,
$ \therefore $ 彩带长度的最小值为 $ 30 \sqrt { 3 } \mathrm { cm } $.
查看更多完整答案,请扫码查看


