第151页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
- 第208页
- 第209页
- 第210页
- 第211页
- 第212页
- 第213页
- 第214页
- 第215页
1. 将抛物线 $ y = a(x - h)^2 $ 上下平移,可得到抛物线 $ y = a(x - h)^2 + k $。
(1)当 $ k > 0 $ 时,向上平移 $ k $ 个单位;
(2)当 $ k < 0 $ 时,向______平移 $ |k| $ 个单位。
(1)当 $ k > 0 $ 时,向上平移 $ k $ 个单位;
(2)当 $ k < 0 $ 时,向______平移 $ |k| $ 个单位。
答案:
下
2. 二次函数 $ y = a(x - h)^2 + k $ 的图象:
(1)图象是抛物线。
(2)当 $ a > 0 $ 时,开口______;当 $ a < 0 $ 时,开口______。
(3)对称轴:直线 $ x = $______。
(4)顶点坐标:______。
(1)图象是抛物线。
(2)当 $ a > 0 $ 时,开口______;当 $ a < 0 $ 时,开口______。
(3)对称轴:直线 $ x = $______。
(4)顶点坐标:______。
答案:
(2)向上 向下
(3)h
(4)(h,k)
(2)向上 向下
(3)h
(4)(h,k)
3. 二次函数 $ y = a(x - h)^2 + k $ 的性质:
(1)当 $ a > 0 $ 时,图象在对称轴左边的部分,函数值 $ y $ 随自变量 $ x $ 取值的增大而______;图象在对称轴右边的部分,函数值 $ y $ 随自变量 $ x $ 取值的增大而______;当 $ x = h $ 时,函数有最______值,其值为______。
(2)当 $ a < 0 $ 时,图象在对称轴左边的部分,函数值 $ y $ 随自变量 $ x $ 取值的增大而______;图象在对称轴右边的部分,函数值 $ y $ 随自变量 $ x $ 取值的增大而______;当 $ x = h $ 时,函数有最______值,其值为______。
(1)当 $ a > 0 $ 时,图象在对称轴左边的部分,函数值 $ y $ 随自变量 $ x $ 取值的增大而______;图象在对称轴右边的部分,函数值 $ y $ 随自变量 $ x $ 取值的增大而______;当 $ x = h $ 时,函数有最______值,其值为______。
(2)当 $ a < 0 $ 时,图象在对称轴左边的部分,函数值 $ y $ 随自变量 $ x $ 取值的增大而______;图象在对称轴右边的部分,函数值 $ y $ 随自变量 $ x $ 取值的增大而______;当 $ x = h $ 时,函数有最______值,其值为______。
答案:
(1)减小 增大 小 k
(2)增大 减小 大 k
(1)减小 增大 小 k
(2)增大 减小 大 k
1. 二次函数 $ y = (x + 2)^2 - 1 $ 的图象大致为( )。
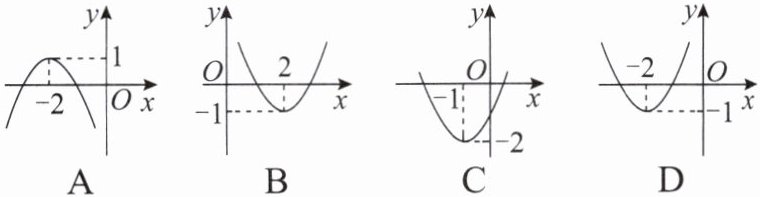

答案:
D
2. 关于抛物线 $ y = -3(x - 1)^2 + 5 $,下列说法正确的是( )。
A.开口向上
B.顶点坐标为 $ (-1, 5) $
C.当 $ x > 1 $ 时,$ y $ 随 $ x $ 的增大而减小
D.将抛物线向上平移 $ 2 $ 个单位后经过原点
A.开口向上
B.顶点坐标为 $ (-1, 5) $
C.当 $ x > 1 $ 时,$ y $ 随 $ x $ 的增大而减小
D.将抛物线向上平移 $ 2 $ 个单位后经过原点
答案:
C 提示:抛物线$y=-3(x-1)^2+5$的顶点坐标为(1,5),a=-3<0,抛物线开口向下.故选项A,B错误.当x≥1时,y随x的增大而减小,故选项C正确.将该抛物线向上平移2个单位,可得$y=-3(x-1)^2+5+2=-3(x-1)^2+7.$当x=0时,y=4,不经过原点,故选项D错误.
3. 在平面直角坐标系中,将二次函数 $ y = x^2 $ 的图象向左平移 $ 2 $ 个单位,再向上平移 $ 1 $ 个单位,所得抛物线所表示的函数表达式为______。
答案:
$y=(x+2)^2+1$
例 (教材第 15 页例 5 变式)已知二次函数图象的顶点坐标为 $ (1, -4) $,且与 $ y $ 轴的交点坐标为 $ (0, -3) $。
(1)求这个二次函数的表达式。
(2)画出(1)中二次函数的图象,并回答问题。
① 它可由抛物线 $ y = x^2 $ 经过怎样的变换得到?
② $ P(x_1, y_1) $,$ Q(x_2, y_2) $ 是抛物线上的两点,且 $ x_1 < x_2 < 1 $,比较 $ y_1 $ 与 $ y_2 $ 的大小。
思路点拨 (1)已知二次函数图象的顶点坐标,可设二次函数的表达式为顶点式,再根据已知条件求出未知系数,即得二次函数的表达式。
(2)根据画二次函数 $ y = a(x - h)^2 + k $ 图象的步骤画出函数图象,并根据图象判断其性质。
解 (1)由于点 $ (1, -4) $ 是二次函数图象的顶点,可设这个二次函数的表达式为 $ y = a(x - 1)^2 - 4 $。
由函数的图象经过点 $ (0, -3) $,可得 $ a(0 - 1)^2 - 4 = -3 $。解得 $ a = 1 $。
因此,这个二次函数的表达式为 $ y = (x - 1)^2 - 4 $。
(2)对称轴是直线 $ x = 1 $,顶点坐标为 $ (1, -4) $。
列表:自变量 $ x $ 从顶点横坐标 $ 1 $ 开始取值。
| $ x $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | …$ $ |
| $ y = (x - 1)^2 - 4 $ | $ -4 $ | $ -3 $ | $ 0 $ | $ 5 $ | …$ $ |
描点和连线:先画出图象在对称轴右边的部分,再利用对称性,画出图象在对称轴左边的部分,如图 1。
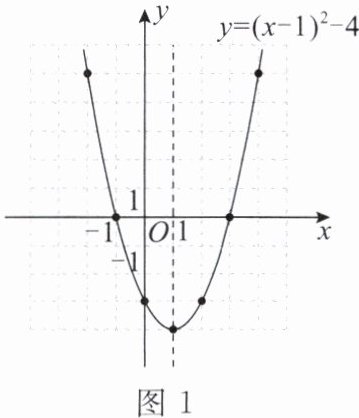
① 由图象可知,抛物线 $ y = (x - 1)^2 - 4 $ 可由抛物线 $ y = x^2 $ 向右平移 $ 1 $ 个单位,再向下平移 $ 4 $ 个单位得到。
② 由图象可知,当 $ x < 1 $ 时,函数值 $ y $ 随自变量 $ x $ 的增大而减小。
因为 $ x_1 < x_2 < 1 $,所以 $ y_1 > y_2 $。
(1)求这个二次函数的表达式。
(2)画出(1)中二次函数的图象,并回答问题。
① 它可由抛物线 $ y = x^2 $ 经过怎样的变换得到?
② $ P(x_1, y_1) $,$ Q(x_2, y_2) $ 是抛物线上的两点,且 $ x_1 < x_2 < 1 $,比较 $ y_1 $ 与 $ y_2 $ 的大小。
思路点拨 (1)已知二次函数图象的顶点坐标,可设二次函数的表达式为顶点式,再根据已知条件求出未知系数,即得二次函数的表达式。
(2)根据画二次函数 $ y = a(x - h)^2 + k $ 图象的步骤画出函数图象,并根据图象判断其性质。
解 (1)由于点 $ (1, -4) $ 是二次函数图象的顶点,可设这个二次函数的表达式为 $ y = a(x - 1)^2 - 4 $。
由函数的图象经过点 $ (0, -3) $,可得 $ a(0 - 1)^2 - 4 = -3 $。解得 $ a = 1 $。
因此,这个二次函数的表达式为 $ y = (x - 1)^2 - 4 $。
(2)对称轴是直线 $ x = 1 $,顶点坐标为 $ (1, -4) $。
列表:自变量 $ x $ 从顶点横坐标 $ 1 $ 开始取值。
| $ x $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | …$ $ |
| $ y = (x - 1)^2 - 4 $ | $ -4 $ | $ -3 $ | $ 0 $ | $ 5 $ | …$ $ |
描点和连线:先画出图象在对称轴右边的部分,再利用对称性,画出图象在对称轴左边的部分,如图 1。

① 由图象可知,抛物线 $ y = (x - 1)^2 - 4 $ 可由抛物线 $ y = x^2 $ 向右平移 $ 1 $ 个单位,再向下平移 $ 4 $ 个单位得到。
② 由图象可知,当 $ x < 1 $ 时,函数值 $ y $ 随自变量 $ x $ 的增大而减小。
因为 $ x_1 < x_2 < 1 $,所以 $ y_1 > y_2 $。
答案:
(1) 设二次函数的表达式为 $y = a(x - 1)^2 - 4$。
代入点 $(0, -3)$,得 $a(0 - 1)^2 - 4 = -3$,解得 $a = 1$。
因此,二次函数的表达式为 $y = (x - 1)^2 - 4$。
(2)
①对称轴是直线 $x = 1$,顶点坐标为 $(1, -4)$。
列表:
| $x$ | $\ldots$ | $-1$ | $0$ | $1$ | $2$ | $3$ | $\ldots$ |
| $y = (x - 1)^2 - 4$ | $\ldots$ | $0$ | $-3$ | $-4$ | $-3$ | $0$ | $\ldots$ |
描点、连线,画出函数图象。
由图象可知,抛物线 $y = (x - 1)^2 - 4$ 可由抛物线 $y = x^2$ 向右平移 $1$ 个单位,再向下平移 $4$ 个单位得到。
② 由于当 $x < 1$ 时,函数值 $y$ 随自变量 $x$ 的增大而减小,且 $x_1 < x_2 < 1$,所以 $y_1 > y_2$。
(1) 设二次函数的表达式为 $y = a(x - 1)^2 - 4$。
代入点 $(0, -3)$,得 $a(0 - 1)^2 - 4 = -3$,解得 $a = 1$。
因此,二次函数的表达式为 $y = (x - 1)^2 - 4$。
(2)
①对称轴是直线 $x = 1$,顶点坐标为 $(1, -4)$。
列表:
| $x$ | $\ldots$ | $-1$ | $0$ | $1$ | $2$ | $3$ | $\ldots$ |
| $y = (x - 1)^2 - 4$ | $\ldots$ | $0$ | $-3$ | $-4$ | $-3$ | $0$ | $\ldots$ |
描点、连线,画出函数图象。
由图象可知,抛物线 $y = (x - 1)^2 - 4$ 可由抛物线 $y = x^2$ 向右平移 $1$ 个单位,再向下平移 $4$ 个单位得到。
② 由于当 $x < 1$ 时,函数值 $y$ 随自变量 $x$ 的增大而减小,且 $x_1 < x_2 < 1$,所以 $y_1 > y_2$。
查看更多完整答案,请扫码查看


