《2025年智慧学习明天出版社九年级数学全一册人教版》

1. 人们用语言来表达对美好事物的赞美或向往时,常常与“圆”字联系在一起,如“花好月圆”“破镜重圆”等。在你的印象里,圆是一个什么样的图形？举例说明在日常生活中,哪些物体是圆形的。
 

答案： 圆是由一条曲线围成的封闭图形，这条曲线上的所有点到定点（圆心）的距离都等于定长（半径）。
在日常生活中，是圆形的物体有：奥运五环、杯口、钟面等（答案不唯一，合理即可，如车轮、碗口等）。

2. 思考：车轮为什么做成圆形？试想一下,如果车轮做成椭圆或正方形,坐车的人会是什么感觉？

答案： 车轮做成圆形，是因为圆上任意一点到圆心的距离都相等（即半径相等）。当车轮滚动时，车轴（圆心）到地面的距离始终等于半径，保持车辆平稳。
若车轮为椭圆，椭圆上点到中心距离不相等，车轴到地面距离不断变化，人会感到颠簸；若为正方形，正方形顶点到中心距离大于边中点到中心距离，滚动时车轴忽高忽低，人会有强烈颠簸感。

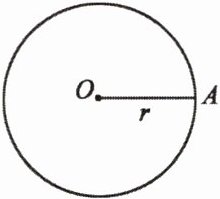
3. 圆的定义：如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆。其固定的端点O叫做圆心,线段OA叫做半径。

答案： 圆；圆心；半径

4. 圆的表示方法：以点O为圆心的圆,记作$\odot O$,读作“圆O”。

答案： 以点O为圆心的圆，记作$\odot O$，读作“圆O”。

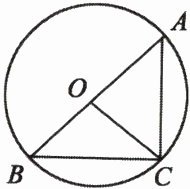
5. 如图,在$\odot O$中,AB过圆心O,则图中的弦有AB,AC,BC,最长的弦是AB,劣弧有$\overset{\frown}{AC}$,$\overset{\frown}{BC}$,以C为端点的优弧有$\overset{\frown}{CAB}$,$\overset{\frown}{CBA}$。

答案： AB, AC, BC；AB；$\overset{\frown}{AC}$, $\overset{\frown}{BC}$；$\overset{\frown}{CAB}$, $\overset{\frown}{CBA}$

1. 自学教科书第79页至第80页例1前的内容,然后回答：
(1)用圆规画一个圆,标明圆心、半径,体会圆的形成过程,思考：圆的位置与什么有关系？圆的大小与什么有关系？
注意：①圆指的是在一个平面内,圆不是球,球也不是圆；
②在画圆的过程中,端点O的位置、线段OA的大小可不可以改变呢？
③在旋转过程中,若旋转不到一周,会出现怎样的情况？
④圆指的是圆周,而非圆面。
圆的位置与圆心有关，圆的大小与半径有关；画圆过程中，圆心位置和半径大小不可改变；旋转不到一周会出现圆弧。
(2)圆这条优美的曲线可以看作是由无数个点组成的图形,而这些点有一个共同的特点：到固定点圆心的距离都相等。
 2. 自学教科书第80页例1后面的内容。
(1)概念学习：
①连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径。
②在同圆或等圆中,能够重合的弧叫做等弧,能够完全重合的两个圆叫做等圆。
(2)概念辨析：
①直径是弦,弦是直径。(×)
②半圆是弧,弧是半圆。(×)
③等于半径两倍的线段是直径。(×)
④过圆心的线段是直径。(×)
⑤过圆心的直线是直径。(×)
⑥半圆是最长的弧。(×)
⑦直径是最长的弦。(√)
⑧圆心相同,半径不相等的两个圆是同心圆。(√)
⑨半径相等的两个圆是等圆。(√)
⑩圆的一条弦所对的两条弧必为一条优弧,一条劣弧。(×)
(3)思考：一个圆上可画出多少条弦？这些弦的长度有范围吗？
一个圆上可以画出无数条弦，弦的长度范围是$0 ＜ l \leq 2r$（$r$为圆的半径）。

答案：
(1) 圆的位置与圆心有关，圆的大小与半径有关；画圆过程中，圆心位置和半径大小不可改变；旋转不到一周会出现圆弧。
(2)
(1) ①线段；弦；重合；完全重合；
(2) ①×；②×；③×；④×；⑤×；⑥×；⑦√；⑧√；⑨√；⑩×；
(3)一个圆上可以画出无数条弦，弦的长度范围是$0 ＜ l \leq 2r$（$r$为圆的半径）。