第136页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
2. 掷一枚质地均匀的骰子有几种可能的结果?点数大于3且小于6的概率是多少?
答案:
答题卡作答:
掷一枚质地均匀的骰子,共有6种可能的结果(即点数1, 2, 3, 4, 5, 6)。
点数大于3且小于6的情况有:4,5,共2种。
所以,$P(点数大于3且小于6) = \frac{2}{6} = \frac{1}{3}$。
掷一枚质地均匀的骰子,共有6种可能的结果(即点数1, 2, 3, 4, 5, 6)。
点数大于3且小于6的情况有:4,5,共2种。
所以,$P(点数大于3且小于6) = \frac{2}{6} = \frac{1}{3}$。
例1 掷两枚硬币,求下列事件的概率:
(1) 两枚硬币全部正面朝上;
(2) 两枚硬币全部反面朝上;
(3) 一枚硬币正面朝上,一枚硬币反面朝上.
分析:我们不妨设其中一枚为A,另一枚为B,则试验的结果为 $ A_{正}B_{正} $,$ A_{正}B_{反} $,$ A_{反}B_{正} $,$ A_{反}B_{反} $,共四种可能.
(1) 两枚硬币全部正面朝上;
(2) 两枚硬币全部反面朝上;
(3) 一枚硬币正面朝上,一枚硬币反面朝上.
分析:我们不妨设其中一枚为A,另一枚为B,则试验的结果为 $ A_{正}B_{正} $,$ A_{正}B_{反} $,$ A_{反}B_{正} $,$ A_{反}B_{反} $,共四种可能.
答案:
答题卡:
解:掷两枚硬币,所有可能的结果有:
$A_{正}B_{正}$,$A_{正}B_{反}$,$A_{反}B_{正}$,$A_{反}B_{反}$。
共4种等可能结果。
(1) 两枚硬币全部正面朝上的情况只有1种,即$A_{正}B_{正}$。
所以$P(两枚全部正面朝上) = \frac{1}{4}$。
(2) 两枚硬币全部反面朝上的情况也只有1种,即$A_{反}B_{反}$。
所以$P(两枚全部反面朝上) = \frac{1}{4}$。
(3) 一枚硬币正面朝上,一枚硬币反面朝上的情况有2种:$A_{正}B_{反}$和$A_{反}B_{正}$。
所以$P(一枚正面朝上,一枚反面朝上) = \frac{2}{4} = \frac{1}{2}$。
解:掷两枚硬币,所有可能的结果有:
$A_{正}B_{正}$,$A_{正}B_{反}$,$A_{反}B_{正}$,$A_{反}B_{反}$。
共4种等可能结果。
(1) 两枚硬币全部正面朝上的情况只有1种,即$A_{正}B_{正}$。
所以$P(两枚全部正面朝上) = \frac{1}{4}$。
(2) 两枚硬币全部反面朝上的情况也只有1种,即$A_{反}B_{反}$。
所以$P(两枚全部反面朝上) = \frac{1}{4}$。
(3) 一枚硬币正面朝上,一枚硬币反面朝上的情况有2种:$A_{正}B_{反}$和$A_{反}B_{正}$。
所以$P(一枚正面朝上,一枚反面朝上) = \frac{2}{4} = \frac{1}{2}$。
例2 同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1) 两枚骰子的点数相同;
(2) 两枚骰子的点数的和是9;
(3) 至少有一枚骰子的点数为2.
分析:此题涉及两个因素(两枚骰子),通常用列表法求两步试验的随机事件的概率.
其表格通常设计为
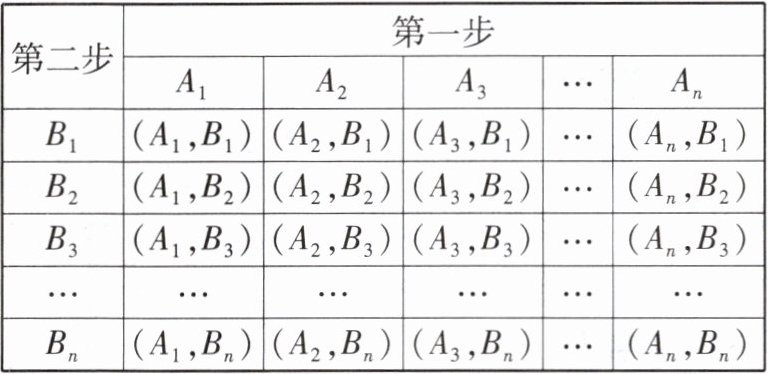
(1) 用表格列举出所有可能出现的结果.
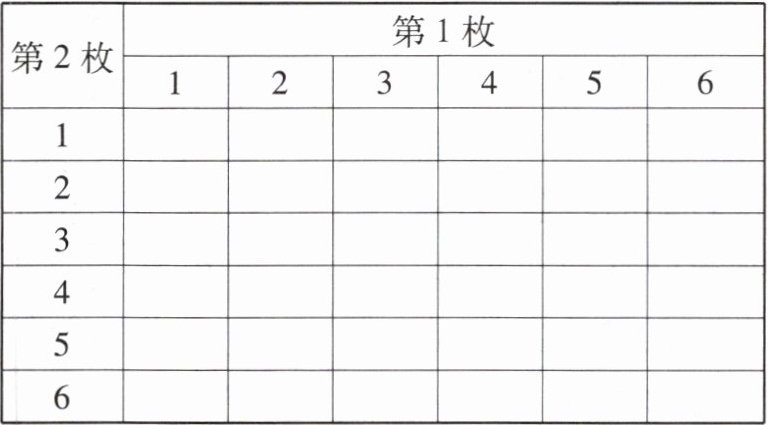
(2) 求出上述各事件的概率.
(3) 思考:将题中的“同时掷两枚骰子”改为“把一枚骰子掷两次”,所得的结果有变化吗?
(4) 从1,2,3,4,5,6中任取两个数,求取到的两个数的和为9的概率.
(1)所有可能结果表格:
| 第2枚 | 第1枚 | 1 | 2 | 3 | 4 | 5 | 6 |
|-------|-------|---------|---------|---------|---------|---------|---------|
| 1 | | (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
| 2 | | (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
| 3 | | (1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) |
| 4 | | (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
| 5 | | (1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) |
| 6 | | (1,6) | (2,6) | (3,6) | (4,6) | (5,6) | (6,6) |
共有36种等可能结果。
(2)各事件概率:
(1)两枚骰子点数相同的结果有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种。$P=\frac{6}{36}=\frac{1}{6}$。
(2)点数和为9的结果有(3,6),(4,5),(5,4),(6,3),共4种。$P=\frac{4}{36}=\frac{1}{9}$。
(3)至少有一枚点数为2的结果有(1,2),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(4,2),(5,2),(6,2),共11种。$P=\frac{11}{36}$。
(3)结果无变化。
(4)任取两数,样本空间为$C_6^2=15$种,和为9的组合有(3,6),(4,5),共2种。$P=\frac{2}{15}$。
(1) 两枚骰子的点数相同;
(2) 两枚骰子的点数的和是9;
(3) 至少有一枚骰子的点数为2.
分析:此题涉及两个因素(两枚骰子),通常用列表法求两步试验的随机事件的概率.
其表格通常设计为

(1) 用表格列举出所有可能出现的结果.

(2) 求出上述各事件的概率.
(3) 思考:将题中的“同时掷两枚骰子”改为“把一枚骰子掷两次”,所得的结果有变化吗?
(4) 从1,2,3,4,5,6中任取两个数,求取到的两个数的和为9的概率.
(1)所有可能结果表格:
| 第2枚 | 第1枚 | 1 | 2 | 3 | 4 | 5 | 6 |
|-------|-------|---------|---------|---------|---------|---------|---------|
| 1 | | (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
| 2 | | (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
| 3 | | (1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) |
| 4 | | (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
| 5 | | (1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) |
| 6 | | (1,6) | (2,6) | (3,6) | (4,6) | (5,6) | (6,6) |
共有36种等可能结果。
(2)各事件概率:
(1)两枚骰子点数相同的结果有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种。$P=\frac{6}{36}=\frac{1}{6}$。
(2)点数和为9的结果有(3,6),(4,5),(5,4),(6,3),共4种。$P=\frac{4}{36}=\frac{1}{9}$。
(3)至少有一枚点数为2的结果有(1,2),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(4,2),(5,2),(6,2),共11种。$P=\frac{11}{36}$。
(3)结果无变化。
(4)任取两数,样本空间为$C_6^2=15$种,和为9的组合有(3,6),(4,5),共2种。$P=\frac{2}{15}$。
答案:
(1)所有可能结果表格:
| 第2枚 | 第1枚 | 1 | 2 | 3 | 4 | 5 | 6 |
|-------|-------|---------|---------|---------|---------|---------|---------|
| 1 | | (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
| 2 | | (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
| 3 | | (1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) |
| 4 | | (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
| 5 | | (1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) |
| 6 | | (1,6) | (2,6) | (3,6) | (4,6) | (5,6) | (6,6) |
共有36种等可能结果。
(2)各事件概率:
(1)两枚骰子点数相同的结果有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种。$P=\frac{6}{36}=\frac{1}{6}$。
(2)点数和为9的结果有(3,6),(4,5),(5,4),(6,3),共4种。$P=\frac{4}{36}=\frac{1}{9}$。
(3)至少有一枚点数为2的结果有(1,2),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(4,2),(5,2),(6,2),共11种。$P=\frac{11}{36}$。
(3)结果无变化。
(4)任取两数,样本空间为$C_6^2=15$种,和为9的组合有(3,6),(4,5),共2种。$P=\frac{2}{15}$。
| 第2枚 | 第1枚 | 1 | 2 | 3 | 4 | 5 | 6 |
|-------|-------|---------|---------|---------|---------|---------|---------|
| 1 | | (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
| 2 | | (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
| 3 | | (1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) |
| 4 | | (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
| 5 | | (1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) |
| 6 | | (1,6) | (2,6) | (3,6) | (4,6) | (5,6) | (6,6) |
共有36种等可能结果。
(2)各事件概率:
(1)两枚骰子点数相同的结果有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种。$P=\frac{6}{36}=\frac{1}{6}$。
(2)点数和为9的结果有(3,6),(4,5),(5,4),(6,3),共4种。$P=\frac{4}{36}=\frac{1}{9}$。
(3)至少有一枚点数为2的结果有(1,2),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(4,2),(5,2),(6,2),共11种。$P=\frac{11}{36}$。
(3)结果无变化。
(4)任取两数,样本空间为$C_6^2=15$种,和为9的组合有(3,6),(4,5),共2种。$P=\frac{2}{15}$。
某联欢会上,组织者为活跃气氛,设计了以下转盘游戏:A,B两个带指针的转盘分别被分成三个面积相等的扇形,转盘A上的数字分别是1,6,8,转盘B上是4,5,7(两个转盘除表面数字不同外,其他完全相同). 选择2名同学分别转动A,B两个转盘,停止后指针所指数字较大的一方为获胜者,另一方需表演节目(若箭头恰好停留在分界线上,则重转一次). 作为游戏者,你会选择哪个装置呢?请说明理由.
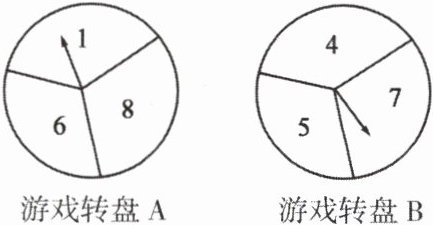

答案:
1. 列出所有可能结果:转盘A有数字1,6,8,转盘B有数字4,5,7,所有等可能结果为(1,4),(1,5),(1,7),(6,4),(6,5),(6,7),(8,4),(8,5),(8,7),共9种。
2. 计算A获胜的情况:A数字大于B数字的结果有(6,4),(6,5),(8,4),(8,5),(8,7),共5种。
3. 计算B获胜的情况:B数字大于A数字的结果有(1,4),(1,5),(1,7),(6,7),共4种。
4. 计算概率:P(A获胜)=5/9,P(B获胜)=4/9。
5. 比较概率:5/9>4/9,故选择转盘A。
结论:选择A装置。
2. 计算A获胜的情况:A数字大于B数字的结果有(6,4),(6,5),(8,4),(8,5),(8,7),共5种。
3. 计算B获胜的情况:B数字大于A数字的结果有(1,4),(1,5),(1,7),(6,7),共4种。
4. 计算概率:P(A获胜)=5/9,P(B获胜)=4/9。
5. 比较概率:5/9>4/9,故选择转盘A。
结论:选择A装置。
查看更多完整答案,请扫码查看


