《2025年智慧学习明天出版社九年级数学全一册人教版》

二、频率与概率的联系与区别.
自学教科书第 143 页“思考”至第 146 页“练习”的内容,回答下列问题：
1. 对于一个随机事件 $ A $,用频率估计的概率 $ P(A) $ 可能小于 $ 0 $ 吗？可能大于 $ 1 $ 吗？
答：对于随机事件$A$，用频率估计的概率$P(A)$不可能小于$0$，也不可能大于$1$。因为概率是反映事件发生可能性大小的量，其取值范围是$[0,1]$。
2. 概率是针对大量重复试验而言的,大量试验反映的规律并非在每一次实验中一定存在.
例如：小芳抛一枚硬币 $ 10 $ 次,有 $ 7 $ 次正面朝上,当她抛第 $ 11 $ 次时,正面朝上的概率为$\frac{1}{2}$.
3. 频率与概率的联系与区别：
联系：当实验次数很多时,事件发生的频率稳定在相应概率的附近,因此可以通过大量多次实验,用一个事件发生的频率来估计这一事件发生的概率.
区别：某随机事件发生的概率是一个定值,而这一事件发生的频率是波动的. 当实验次数不多时,事件发生的频率与概率的差异甚至很大.
答：联系：当试验次数很多时，事件发生的频率稳定在相应概率的附近，因此可以通过大量多次试验，用一个事件发生的频率来估计这一事件发生的概率。
区别：某随机事件发生的概率是一个定值，而这一事件发生的频率是波动的。当试验次数不多时，事件发生的频率与概率的差异甚至很大。

答案： 1.
答：对于随机事件$A$，用频率估计的概率$P(A)$不可能小于$0$，也不可能大于$1$。因为概率是反映事件发生可能性大小的量，其取值范围是$[0,1]$。
2.
答：$\frac{1}{2}$。抛硬币每次正面朝上或反面朝上的概率都是固定的，与抛的次数无关，每次抛硬币正面朝上的概率都是$\frac{1}{2}$。
3.
答：联系：当试验次数很多时，事件发生的频率稳定在相应概率的附近，因此可以通过大量多次试验，用一个事件发生的频率来估计这一事件发生的概率。
区别：某随机事件发生的概率是一个定值，而这一事件发生的频率是波动的。当试验次数不多时，事件发生的频率与概率的差异甚至很大。

例 1 某林业部门要考查某种幼树在一定条件下的移植成活率,应采用什么具体做法？观察在各次试验中得到的幼树成活的频率,谈谈你的看法.
由教科书上的表格可以发现,幼树移植成活的频率在0.9（或 90% ）左右摆动,并且随着移植棵数越来越大,这种规律愈加明显.
(1)林业部门种植了该幼树 1000 棵,估计能成活900棵.
(2)我们学校需种植这样的树苗 500 棵来绿化校园,则至少向林业部门购买幼树约556棵.

答案： $0.9$（或 $90\%$ ）；900；556。

例 2 某商场为了吸引顾客,举行抽奖活动,并规定：顾客每购买 $ 100 $ 元的商品,就可以随机抽取一张奖券,抽得奖券“紫气东来”“花开富贵”“吉星高照”,就可以分别获得 $ 100 $ 元,$ 50 $ 元,$ 20 $ 元的购物券,抽得“谢谢惠顾”不赠购物券；如果顾客不愿意抽奖,可以直接获得 $ 10 $ 元的购物券. 小明购买了 $ 100 $ 元的商品,他看到商场公布的前 $ 10000 $ 张奖券的抽奖结果如下：

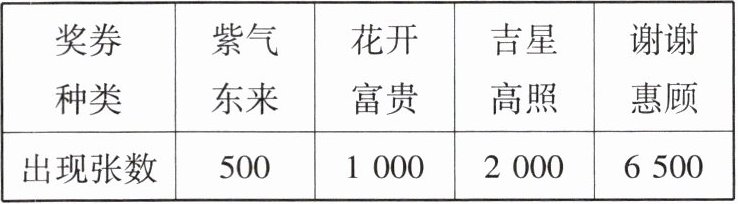
(1)求“紫气东来”奖券出现的频率；
(2)请你帮助小明判断：抽奖和直接获得购物券,哪种方式更合算？说明理由.

答案：
(1)“紫气东来”奖券出现的频率为：$\frac{500}{10000}=0.05$
(2)抽奖获得购物券的平均金额为：
$\begin{aligned}&100×\frac{500}{10000}+50×\frac{1000}{10000}+20×\frac{2000}{10000}+0×\frac{6500}{10000}\\=&100×0.05 + 50×0.1 + 20×0.2 + 0\\=&5 + 5 + 4\\=&14(元)\end{aligned}$
因为$14＞10$，所以抽奖更合算。
(1)0.05；
(2)抽奖更合算。