第175页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
2.【数学与生活融合项目式学习】山西省首座独塔悬索桥——通达桥,全长 $ 1.54 \mathrm{~km} $,主桥横跨汾河,全长 $ 416 \mathrm{~m} $,宽 $ 45 \mathrm{~m} $,是太原新建成的一座跨河大桥,桥的主塔由曲线形拱门组成,取意“时代之门”.某数学“综合与实践”小组把“测量通达桥拱门的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间完成了实地测量,测量结果如表:
|项目|测量通达桥拱门的高度|
|----|----|
|测量示意图及说明| |说明:他们利用无人机技术进行测量,$ AB $ 代表通达桥拱门,$ C,D $ 是两个观测点,已知 $ CD \perp BM $,$ AB \perp BM $,点 $ A,B,C,D $ 在同一平面内,$ BM $ 为桥面|
|说明:他们利用无人机技术进行测量,$ AB $ 代表通达桥拱门,$ C,D $ 是两个观测点,已知 $ CD \perp BM $,$ AB \perp BM $,点 $ A,B,C,D $ 在同一平面内,$ BM $ 为桥面|
|测量数据|点 $ C $ 处的仰角|点 $ D $ 处的俯角|观测点 $ C $ 距桥面的高度|点 $ D,C $ 之间的距离|
| | $ 30^{\circ} $| $ 45^{\circ} $| $ 50 \mathrm{~m} $| $ 200 \mathrm{~m} $|
|...|...|
任务一:请运用你所学的知识,根据表中的测量数据,帮助“综合与实践”小组求出通达桥拱门的高度 $ AB $;(结果保留整数,参考数据:$ \sqrt{3} \approx 1.73 $,$ \sqrt{2} \approx 1.41 $)
任务二:请你根据所学的知识,再设计一种方案,画出示意图,并写出需要测量的量.
|项目|测量通达桥拱门的高度|
|----|----|
|测量示意图及说明|
 |说明:他们利用无人机技术进行测量,$ AB $ 代表通达桥拱门,$ C,D $ 是两个观测点,已知 $ CD \perp BM $,$ AB \perp BM $,点 $ A,B,C,D $ 在同一平面内,$ BM $ 为桥面|
|说明:他们利用无人机技术进行测量,$ AB $ 代表通达桥拱门,$ C,D $ 是两个观测点,已知 $ CD \perp BM $,$ AB \perp BM $,点 $ A,B,C,D $ 在同一平面内,$ BM $ 为桥面||测量数据|点 $ C $ 处的仰角|点 $ D $ 处的俯角|观测点 $ C $ 距桥面的高度|点 $ D,C $ 之间的距离|
| | $ 30^{\circ} $| $ 45^{\circ} $| $ 50 \mathrm{~m} $| $ 200 \mathrm{~m} $|
|...|...|
任务一:请运用你所学的知识,根据表中的测量数据,帮助“综合与实践”小组求出通达桥拱门的高度 $ AB $;(结果保留整数,参考数据:$ \sqrt{3} \approx 1.73 $,$ \sqrt{2} \approx 1.41 $)
任务二:请你根据所学的知识,再设计一种方案,画出示意图,并写出需要测量的量.
答案:
解: 任务一: 如图 1, 延长 $ D C $ 交 $ B M $ 于点 $ N $, 过点 $ A $ 作 $ A P \perp D C $ 于点 $ P $,
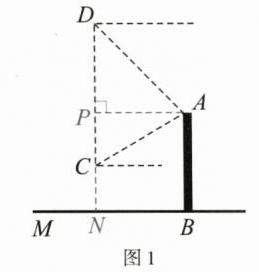
$ \because C D \perp B M, A B \perp B M $,
$ \therefore \angle A P N = \angle P N B = \angle A B N = 90 ^ { \circ } $.
$ \therefore $ 四边形 $ A P N B $ 为矩形.
$ \therefore A B = P N $.
依题意, 得
$ \angle A C P = 90 ^ { \circ } - 30 ^ { \circ } = 60 ^ { \circ } $,
$ \angle A D P = 90 ^ { \circ } - 45 ^ { \circ } = 45 ^ { \circ } $,
$ C N = 50 m, D C = 200 m $,
在 $ Rt\triangle A P D $ 中,
$ \tan \angle A D P = \tan 45 ^ { \circ } = \frac { A P } { D P } = 1 $,
$ \therefore A P = D P $.
在 $ Rt\triangle A P C $ 中,
$ \tan \angle A C P = \tan 60 ^ { \circ } = \frac { A P } { P C } = \sqrt { 3 } $,
$ \therefore D P = A P = \sqrt { 3 } P C $.
$ \because D C = 200 m $,
$ \therefore P C + P D = P C + \sqrt { 3 } P C = 200 $.
$ \therefore P C = \frac { 200 } { \sqrt { 3 } + 1 } = 100 ( \sqrt { 3 } - 1 ) \approx 100 × ( 1.73 - 1 ) = 73 ( m ) $.
$ \because C N = 50 m $,
$ \therefore A B = P N = P C + C N = 73 + 50 = 123 ( m ) $.
答: 通达桥拱门的高度 $ A B $ 约为 $ 123 m $.
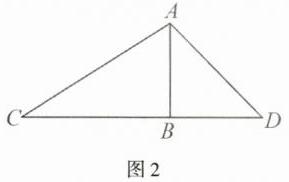
任务二: 测量方案如图 2 所示, 需要测量的量有 $ \angle A C B $ 的度数, $ \angle A D C $ 的度数, 点 $ D, C $ 之间的距离. (答案不唯一)
解: 任务一: 如图 1, 延长 $ D C $ 交 $ B M $ 于点 $ N $, 过点 $ A $ 作 $ A P \perp D C $ 于点 $ P $,

$ \because C D \perp B M, A B \perp B M $,
$ \therefore \angle A P N = \angle P N B = \angle A B N = 90 ^ { \circ } $.
$ \therefore $ 四边形 $ A P N B $ 为矩形.
$ \therefore A B = P N $.
依题意, 得
$ \angle A C P = 90 ^ { \circ } - 30 ^ { \circ } = 60 ^ { \circ } $,
$ \angle A D P = 90 ^ { \circ } - 45 ^ { \circ } = 45 ^ { \circ } $,
$ C N = 50 m, D C = 200 m $,
在 $ Rt\triangle A P D $ 中,
$ \tan \angle A D P = \tan 45 ^ { \circ } = \frac { A P } { D P } = 1 $,
$ \therefore A P = D P $.
在 $ Rt\triangle A P C $ 中,
$ \tan \angle A C P = \tan 60 ^ { \circ } = \frac { A P } { P C } = \sqrt { 3 } $,
$ \therefore D P = A P = \sqrt { 3 } P C $.
$ \because D C = 200 m $,
$ \therefore P C + P D = P C + \sqrt { 3 } P C = 200 $.
$ \therefore P C = \frac { 200 } { \sqrt { 3 } + 1 } = 100 ( \sqrt { 3 } - 1 ) \approx 100 × ( 1.73 - 1 ) = 73 ( m ) $.
$ \because C N = 50 m $,
$ \therefore A B = P N = P C + C N = 73 + 50 = 123 ( m ) $.
答: 通达桥拱门的高度 $ A B $ 约为 $ 123 m $.
任务二: 测量方案如图 2 所示, 需要测量的量有 $ \angle A C B $ 的度数, $ \angle A D C $ 的度数, 点 $ D, C $ 之间的距离. (答案不唯一)

查看更多完整答案,请扫码查看


