第169页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
9.如图,一条输电线路从$A$地到$B$地需要经过$C$地,图中$AC = 20$千米,$\angle CAB = 30^{\circ}$,$\angle CBA = 45^{\circ}$.因线路整改需要,将从$A$地到$B$地之间铺设一条笔直的输电线路.
(1)求新铺设的输电线路$AB$的长度.
(2)问整改后从$A$地到$B$地的输电线路比原来缩短了多少千米?(结果保留根号)
(1)求新铺设的输电线路$AB$的长度.
(2)问整改后从$A$地到$B$地的输电线路比原来缩短了多少千米?(结果保留根号)
答案:
解:
(1) 如图,过点 C 作 CD⊥AB,交 AB 于点 D,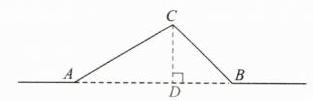
在 Rt△ACD 中,
$CD = \frac{1}{2}AC = \frac{1}{2}×20$
$=10$(千米),
$AD = AC\cdot\cos30^{\circ} = 20×\frac{\sqrt{3}}{2}$
$=10\sqrt{3}$(千米).
又
∵ ∠CBD = 45°,
∴ BD = CD = 10 千米.
∴ AB = AD + DB
$=10\sqrt{3}+10$(千米).
(2)
∵ $BC = \frac{BD}{\cos45^{\circ}}$
$=10\sqrt{2}$(千米),
∴ AC + BC - AB
$=20 + 10\sqrt{2} - (10\sqrt{3} + 10)$
$=(10 + 10\sqrt{2} - 10\sqrt{3})$(千米).
答:整改后,输电线路比原来缩短了$(10 + 10\sqrt{2} - 10\sqrt{3})$千米.
解:
(1) 如图,过点 C 作 CD⊥AB,交 AB 于点 D,

在 Rt△ACD 中,
$CD = \frac{1}{2}AC = \frac{1}{2}×20$
$=10$(千米),
$AD = AC\cdot\cos30^{\circ} = 20×\frac{\sqrt{3}}{2}$
$=10\sqrt{3}$(千米).
又
∵ ∠CBD = 45°,
∴ BD = CD = 10 千米.
∴ AB = AD + DB
$=10\sqrt{3}+10$(千米).
(2)
∵ $BC = \frac{BD}{\cos45^{\circ}}$
$=10\sqrt{2}$(千米),
∴ AC + BC - AB
$=20 + 10\sqrt{2} - (10\sqrt{3} + 10)$
$=(10 + 10\sqrt{2} - 10\sqrt{3})$(千米).
答:整改后,输电线路比原来缩短了$(10 + 10\sqrt{2} - 10\sqrt{3})$千米.
10.(2024·佛山一模)“醒狮”是岭南文化名城佛山的一块闪亮的招牌,是国家非物质文化遗产之一,舞狮者用狮嘴将悬于高处、寓意着吉祥的“生菜”采摘的过程称为“采青”,舞狮者脚站立的位置与狮嘴可触摸到的位置之间的距离称为“采摘距离”.如图,舞狮者站在梅花桩$AB$上,$AB$与“生菜”放置点$D$的水平距离$BC$为$1.1m$,$\angle D = 53^{\circ}$.已知该舞狮者的采摘距离为$1.43m$,请利用所学知识判断该舞狮者能否“采青”成功,并说明理由.(参考数据:$\sin 53^{\circ} \approx 0.8$,$\cos 53^{\circ} \approx 0.6$,$\tan 53^{\circ} \approx 1.3$)
答案:
解:该舞狮者能“采青”成功. 理由如下:
如图,过点 A 作 AE⊥CD,垂足为 E,
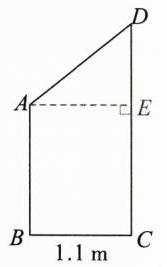
依题意,得 AE = BC = 1.1 m,
在 Rt△AED 中,∠D = 53°,
∴ $AD = \frac{AE}{\sin53^{\circ}} \approx \frac{1.1}{0.8}$
$=1.375$(m).
∵ 1.375 < 1.43,
∴ 该舞狮者能“采青”成功.
解:该舞狮者能“采青”成功. 理由如下:
如图,过点 A 作 AE⊥CD,垂足为 E,

依题意,得 AE = BC = 1.1 m,
在 Rt△AED 中,∠D = 53°,
∴ $AD = \frac{AE}{\sin53^{\circ}} \approx \frac{1.1}{0.8}$
$=1.375$(m).
∵ 1.375 < 1.43,
∴ 该舞狮者能“采青”成功.
11.(2024·梅县区一模)如图所示,某幼儿园为加强安全管理,决定将园内的滑板的倾斜角由$45^{\circ}$降为$30^{\circ}$,已知原滑板$AB$的长为4米,点$D$,$B$,$C$在同一水平地面上.
(1)求改善后滑板$AD$的长为多少米.
(2)若滑板的正前方能有3米长的空地就能保证安全,原滑板的前方有6m长的空地,像这样改造是否可行?请说明理由.(参考数据:$\sqrt{2} \approx 1.414$,$\sqrt{3} \approx 1.732$,$\sqrt{6} \approx 2.449$,以上结果均保留到小数点后两位)
(1)求改善后滑板$AD$的长为多少米.
(2)若滑板的正前方能有3米长的空地就能保证安全,原滑板的前方有6m长的空地,像这样改造是否可行?请说明理由.(参考数据:$\sqrt{2} \approx 1.414$,$\sqrt{3} \approx 1.732$,$\sqrt{6} \approx 2.449$,以上结果均保留到小数点后两位)
答案:
解:
(1) 在 Rt△ABC 中,
$AC = AB\cdot\sin45^{\circ}$
$=4\times\frac{\sqrt{2}}{2} = 2\sqrt{2}$(m),
在 Rt△ADC 中,∠ADC = 30°,
AD = 2AC = $4\sqrt{2} \approx 5.66$(m).
答:改善后滑板 AD 的长约为 5.66 m.
(2) 这样改造可行. 理由如下:
在 Rt△ADC 中,
$CD = \frac{AC}{\tan30^{\circ}} = \frac{2\sqrt{2}}{\frac{\sqrt{3}}{3}} = 2\sqrt{6}$
≈4.898(m),
∵ ∠ABC = 45°,
∴ BC = AC = $2\sqrt{2}$ m.
∴ BD = CD - BC
$=2\sqrt{6} - 2\sqrt{2}$
≈4.898 - 2.828
=2.07(m).
∵ 6 - 2.07 = 3.93 > 3,
∴ 这样改造可行.
(1) 在 Rt△ABC 中,
$AC = AB\cdot\sin45^{\circ}$
$=4\times\frac{\sqrt{2}}{2} = 2\sqrt{2}$(m),
在 Rt△ADC 中,∠ADC = 30°,
AD = 2AC = $4\sqrt{2} \approx 5.66$(m).
答:改善后滑板 AD 的长约为 5.66 m.
(2) 这样改造可行. 理由如下:
在 Rt△ADC 中,
$CD = \frac{AC}{\tan30^{\circ}} = \frac{2\sqrt{2}}{\frac{\sqrt{3}}{3}} = 2\sqrt{6}$
≈4.898(m),
∵ ∠ABC = 45°,
∴ BC = AC = $2\sqrt{2}$ m.
∴ BD = CD - BC
$=2\sqrt{6} - 2\sqrt{2}$
≈4.898 - 2.828
=2.07(m).
∵ 6 - 2.07 = 3.93 > 3,
∴ 这样改造可行.
12.如图,在岷江的右岸边有一座高楼$AB$,左岸边有一坡度$i = 1:2$的山坡$CF$,点$C$与点$B$在同一水平面上,$CF$与$AB$在同一平面内.某数学兴趣小组为了测量楼$AB$的高度,在坡底$C$处测得楼顶$A$的仰角为$45^{\circ}$,然后沿坡面$CF$上行走了$20\sqrt{5}m$到达点$D$处,此时在点$D$处测得楼顶$A$的仰角为$30^{\circ}$,求楼$AB$的高度.
答案:
解:在 Rt△DEC 中,
∵ $i = \frac{DE}{EC} = \frac{1}{2}$,
$DE^{2} + EC^{2} = CD^{2}$,
CD = $20\sqrt{5}$ m,
∴ $DE^{2} + (2DE)^{2} = (20\sqrt{5})^{2}$,
解得 DE = 20 m.
∴ EC = 40 m.
如图,过点 D 作 DG⊥AB 于点 G,
过点 C 作 CH⊥DG 于点 H,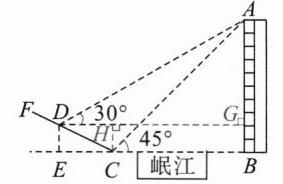
则四边形 DEBG,四边形 DECH,四边形 BCHG 都是矩形.
∵ ∠ACB = 45°,AB⊥BC,
∴ AB = BC.
设 AB = BC = x m,
则 AG = (x - 20)m,
DG = (x + 40)m.
在 Rt△ADG 中,
∵ $\frac{AG}{DG} = \tan∠ADG$,
∴ $\frac{x - 20}{x + 40} = \frac{\sqrt{3}}{3}$,
解得 $x = 50 + 30\sqrt{3}$.
答:楼 AB 的高度为$(50 + 30\sqrt{3})$m.
解:在 Rt△DEC 中,
∵ $i = \frac{DE}{EC} = \frac{1}{2}$,
$DE^{2} + EC^{2} = CD^{2}$,
CD = $20\sqrt{5}$ m,
∴ $DE^{2} + (2DE)^{2} = (20\sqrt{5})^{2}$,
解得 DE = 20 m.
∴ EC = 40 m.
如图,过点 D 作 DG⊥AB 于点 G,
过点 C 作 CH⊥DG 于点 H,

则四边形 DEBG,四边形 DECH,四边形 BCHG 都是矩形.
∵ ∠ACB = 45°,AB⊥BC,
∴ AB = BC.
设 AB = BC = x m,
则 AG = (x - 20)m,
DG = (x + 40)m.
在 Rt△ADG 中,
∵ $\frac{AG}{DG} = \tan∠ADG$,
∴ $\frac{x - 20}{x + 40} = \frac{\sqrt{3}}{3}$,
解得 $x = 50 + 30\sqrt{3}$.
答:楼 AB 的高度为$(50 + 30\sqrt{3})$m.
查看更多完整答案,请扫码查看


