《2025年新课程学习与测评同步学习九年级数学全一册人教版》

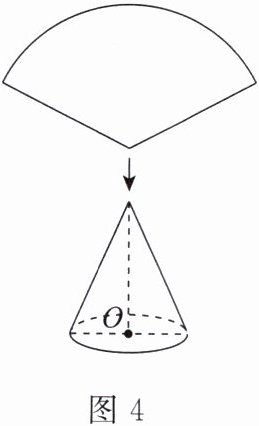
3. 如图4,用一张半径为24 cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),若圆锥形帽子的底面半径为10 cm,则这张扇形纸板的面积是240π$cm^{2}$。(结果保留$\pi$)

答案： $240 \pi$

4. 已知圆锥的底面圆的半径是1,高是$\sqrt{15}$,则该圆锥的侧面展开图的圆心角的度数是90。

答案： $90$（填数字）

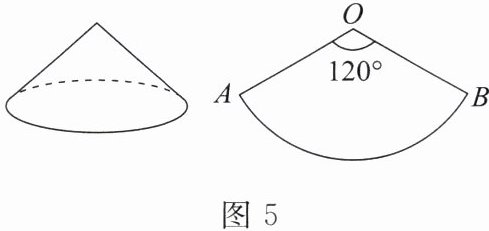
5. 如图5,已知一个圆锥的侧面展开图是一个半径为9 cm,圆心角为$120^{\circ}$的扇形。
求圆锥的底面圆的半径。
求圆锥的全面积。(结果保留$\pi$)

答案：
（1）圆锥底面圆的半径为 $ 3 $ cm；
（2）圆锥的全面积为 $ 36\pi $ cm²。

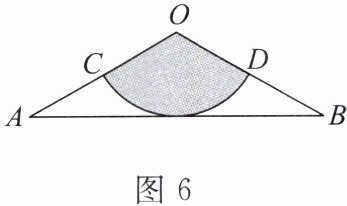
6. 如图6,从一张腰长为60 cm,顶角为$120^{\circ}的等腰三角形铁皮OAB中剪出一个最大的扇形OCD$,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为20√2cm。

答案： 20√2

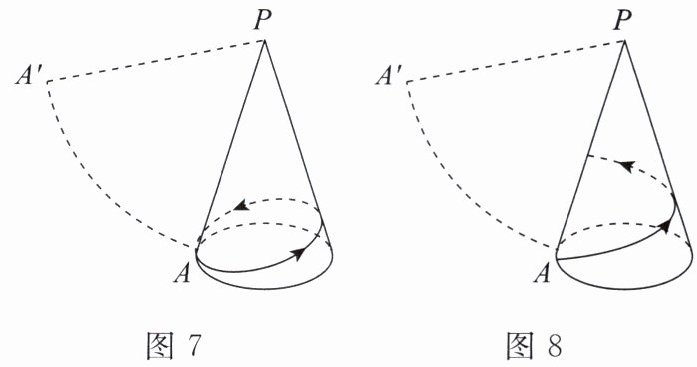
7. 图7是一个底面圆的半径为$\frac{2}{3}$,母线长为4的圆锥和它的侧面展开图扇形$PAA'$,$PA$是它的一条母线。
一只蚂蚁从点$A出发沿圆锥的侧面爬行一周后回到点A$,求蚂蚁爬行的最短路程。
一只蚂蚁从点$A出发沿圆锥的侧面爬行一周到达母线PA$上的一点(如图8),求蚂蚁爬行的最短路程。

答案： 1. 圆锥底面周长：$2\pi r = 2\pi × \frac{2}{3} = \frac{4\pi}{3}$。
2. 设扇形圆心角为$n°$，由弧长公式$\frac{n\pi × 4}{180} = \frac{4\pi}{3}$，解得$n = 60°$。
3. 展开图扇形圆心角$\angle APA' = 60°$，$PA = PA' = 4$，$\triangle APA'$为等边三角形，$AA' = 4$。第一问最短路程为$4$。
4. 过$A$作$PA$垂线，垂足为$M$，最短距离$AM = PA \cdot \sin 60° = 4 × \frac{\sqrt{3}}{2} = 2\sqrt{3}$。第二问最短路程为$2\sqrt{3}$。
4；$2\sqrt{3}$