《2025年零障碍导教导学案八年级数学上册人教版》

8. (新教材 P156 T7)一块麦田有$mhm^{2}$,甲收割完这块麦田需nh,乙比甲少用0.5h就能收割完这块麦田,两人一起收割完这块麦田需要多少小时?

答案： 解:m÷($\frac{m}{n}+\frac{m}{n-0.5}$)
=m÷$\frac{2mn-0.5m}{n(n-0.5)}$
=$\frac{mn(n-0.5)}{2mn-0.5m}=\frac{mn(n-0.5)}{m(2n-0.5)}$
=$\frac{n(n-0.5)}{2n-0.5}=\frac{2n²-n}{4n-1}$(h).
答:两人一起收割完这块麦田需要$\frac{2n²-n}{4n-1}$h.

9. (新教材 P163 T8)通常分子的质量和体积都很小,已知1个水分子的质量约是$3×10^{-26}kg$,1滴水(以 20 滴水为 1 g 计)中大约有多少个水分子? 假设 10 亿人来数 1 滴水中的水分子,每人每分数 100 个,日夜不停,大约需要多长时间才能数完?

答案： 解:1滴水中水分子的个数约为
1÷20×10⁻³÷(3×10⁻²⁶)≈1.67×10²¹.
1.67×10²¹÷10⁹÷100÷60÷24÷365≈31773(年).
∴日夜不停,大约需要31773年才能数完.

10. (新教材 P145 T9)某村种植了$mhm^{2}$玉米,总产量为nkg;水稻的种植面积比玉米的种植面积多$phm^{2}$,水稻的总产量比玉米总产量的 2 倍多 q kg. 写出表示玉米和水稻的单位面积产量(单位:$kg/hm^{2}$)的式子.

答案： 解:
∵玉米种植面积为m hm²,且玉米总产量为n kg,
∴玉米单位面积产量为$\frac{n}{m}$kg/hm².
∵水稻的种植面积为(m+p)hm²,且水稻总产量(2n+q)kg,
∴水稻单位面积产量为$\frac{2n+q}{m+p}$kg/hm².

11. (新教材 P145 T10)有四块小场地:第一块是边长为 a m 的正方形,第二块是边长为b m 的正方形,其余两块都是长为 a m、宽为b m 的长方形. 另有一块大长方形场地,它的面积等于上面四块场地面积的和,它的长为$2(a+b)m$,用最简单的式子表示出大长方形的宽.

答案： 解:四块小场地的面积之和为a²+b²+2ab=(a+b)²(m²),
∴大长方形的宽为$\frac{(a+b)²}{2(a+b)}=\frac{a+b}{2}$(m).

12. (新教材 P173 T6 改编)填空:
(1)当x为____时,分式$\frac {3x-6}{2x+1}$的值为0;
(2)当$x(x≠0)$为____时,分式$\frac {2x+1}{x^{2}}$的值为正;
(3)当$x(x≠0)$为____时,分式$\frac {x-2}{x^{2}}$的值为负.

答案：
(1)2
(2)x＞-$\frac{1}{2}$
(3)x＜2

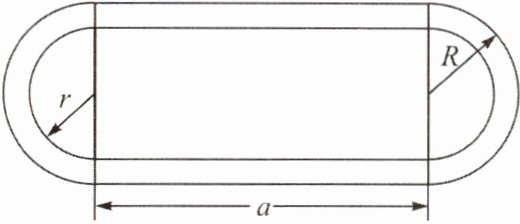
13. (新教材 P173 T12)如图,运动场两端的半圆形跑道外径为 R,内径为 r,中间为直跑道,整个跑道总面积为 S,试用含 S,R,r 的式子表示直跑道的长 a.

答案： 解:
∵圆环跑道面积是π(R²-r²),
两个直跑道的面积是S-$\pi$(R²-r²).
∴a=$\frac{S-\pi(R²-r²)}{2(R-r)}$.

14. (新教材 P173 T13)(1)式子$\frac {a}{bc}+\frac {b}{ca}+\frac {c}{ab}$的值能否为 0? 为什么?
(2)式子$\frac {a-b}{(b-c)(c-a)}+\frac {b-c}{(a-b)(c-a)}+\frac {c-a}{(a-b)(b-c)}$的值能否为 0? 为什么?

答案： 解:
(1)原式=$\frac{a²+b²+c²}{abc}$,不能为0,
若原式为0,则a=b=c=0,此时分式没有意义.
(2)原式=$\frac{(a-b)²+(b-c)²+(c-a)²}{(a-b)(b-c)(c-a)}$,不能为0,若原式0,则a=b=c,此时分式没有意义.

15. (新教材 P151 T10)观察周边生活或查阅书籍,设计一个运用分式乘除运算的实际问题,并给出解答.

答案： 解:实际问题:某工厂用两台机器生产零件.机器A的工作效率为$\frac{a}{b}$个/小时,机器B工作效率是机器A$\frac{c}{d}$.
(1)求机器B的工作效率(用分式表示);
(2)若两台机器同时工作t小时,求它们生产的总零件数(用分式表示).
解答如下:
(1)机器B的工作效率为$\frac{a}{b}·\frac{c}{d}=\frac{ac}{bd}$(个/小时).
(2)它们生产的总零件数为$\frac{at}{b}+\frac{act}{bd}=\frac{adt}{bd}+\frac{act}{bd}=\frac{adt+act}{bd}=\frac{at(d+c)}{bd}$(个).(答案不唯一)