《2025年广东名师讲练通九年级数学全一册北师大版深圳专版》

7. “今有邑, 东西七里, 南北九里, 各开中门, 出东门一十五里有木, 问: 出南门几何步而见木?”这段话摘自《九章算术》, 意思是说: 如图, 矩形城池ABCD, 东边城墙AB长9里, 南边城墙AD长7里, 东门点E, 南门点F分别是AB, AD的中点,$EG\perp AB$,$FH\perp AD$,$EG=15$里, HG经过点A, 求FH.

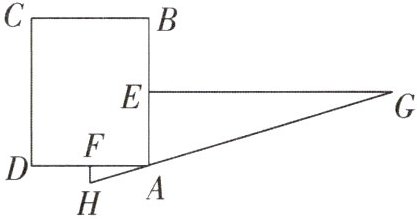
解：∵EG⊥AB，FH⊥AD，HG 经过点 A，∴FA//EG，EA//FH，∴∠AEG=∠HFA=90°，∠EAG=∠FHA，∴△GEA∽△AFH，∴$\frac{GE}{AF}=\frac{AE}{HF}$。∵AB=9 里，AD=7 里，EG=15 里，∴AF=3.5 里，AE=4.5 里，∴$\frac{15}{3.5}=\frac{4.5}{HF}$，∴FH=1.05里。

答案： 解：
∵EG⊥AB，FH⊥AD，HG 经过点 A，
∴FA//EG，EA//FH，
∴∠AEG=∠HFA=90°，∠EAG=∠FHA，
∴△GEA∽△AFH，
∴$\frac{GE}{AF}=\frac{AE}{HF}$。
∵AB=9 里，AD=7 里，EG=15 里，
∴AF=3.5 里，AE=4.5 里，
∴$\frac{15}{3.5}=\frac{4.5}{HF}$，
∴FH=1.05 里。

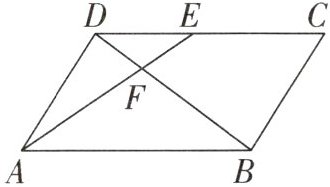
8. 如图, 在平行四边形ABCD中, E为CD上一点, 连接AE, BD, 且AE, BD交于点F,$EF:AF=2:5$, 已知$\triangle DEF$的面积是4, 求四边形BCEF的面积.

(31)

答案： 解：
∵四边形 ABCD 是平行四边形，
∴DE//AB，
∴△DEF∽△BAF。
∵EF:AF=2:5，
∴$\frac{h_{△DEF}}{h_{△BAF}}=\frac{2}{5}$，$\frac{DE}{AB}=\frac{2}{5}$。设 $h_{△DEF}=2k$，DE=2m，AB=5m，
∴$h_{四边形 ABCD}=7k$。
∵△DEF 的面积是 4，
∴$\frac{1}{2}×2m×2k=4$，
∴mk=2，
∴$S_{△DBC}=\frac{1}{2}CD·h_{四边形 ABCD}=\frac{1}{2}×5m×7k=35$，
∴四边形 BCEF 的面积是 31。

9. 如图, P为平行四边形ABCD边BC上一点, E, F分别为PA, PD上的点, 且$AE=2EP$,$DF=2FP$,$\triangle PEF$,$\triangle PDC$,$\triangle PAB$的面积分别记为S,$S_1$,$S_2$, 若$S=a$, 求$S_1+S_2$的值.

9a

答案： 解：如图，过点 D 作 DH⊥BC 于点 H。
∵四边形 ABCD 为平行四边形，
∴AD//BC，AD=BC。
∵$S_1=\frac{1}{2}PC·DH$，$S_2=\frac{1}{2}BP·DH$，
∴$S_1+S_2=\frac{1}{2}(PC+BP)·DH=\frac{1}{2}BC·DH$。又
∵$S_{△PAD}=\frac{1}{2}AD·DH=\frac{1}{2}BC·DH$，
∴$S_1+S_2=S_{△PAD}$。
∵AE=2EP，DF=2FP，
∴$\frac{PE}{PA}=\frac{PF}{PD}=\frac{1}{3}$。又
∵∠EPF=∠APD，
∴△EPF∽△APD，
∴$\frac{S}{S_{△PAD}}=(\frac{1}{3})^2$，
∴$S_{△PAD}=9S=9a$，
∴$S_1+S_2=9a$。

10. 如图,$AE\perp AB$,$AE=AB$,$BC\perp CD$, 且$2BC=CD$,$EF=6$,$BG=4$,$DH=5$, 求图中实线所围成的图形的面积.

$\frac{255}{4}$

答案： 解：
∵AE⊥AB，且 AE=AB，EF⊥AF，BG⊥AG，
∴∠F=∠EAB=∠AGB=90°，
∴∠AEF+∠EAF=90°，∠BAG+∠EAF=90°，
∴∠AEF=∠BAG，
∴△EFA≌△AGB（AAS），
∴AF=BG=4，EF=AG=6。
∵BG⊥CG，DH⊥CH，BC⊥CD，
∴∠BGC=∠BCD=∠H=90°，
∴∠GBC+∠GCB=90°，∠DCH+∠GCB=90°，
∴∠GBC=∠DCH，
∴△BGC∽△CHD，
∴$\frac{BC}{CD}=\frac{BG}{CH}=\frac{GC}{DH}=\frac{1}{2}$，
∴CG=$\frac{5}{2}$，CH=8，$S=S_{梯形 DHFE}−S_{△EFA}−S_{△BCA}−S_{△DHC}=\frac{1}{2}×(5+6)×(4+6+\frac{5}{2}+8)−\frac{1}{2}×6×4−\frac{1}{2}×(6+\frac{5}{2})×4−\frac{1}{2}×8×5=\frac{255}{4}$。