《2025年广东名师讲练通九年级数学全一册北师大版深圳专版》

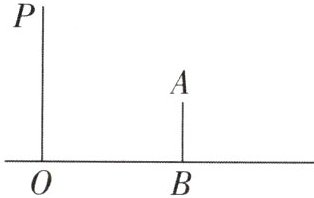
【例3】(2023·佛山联考)如图，晚上，小亮站在广场上乘凉.线段AB表示站立的小亮，线段OP表示广场上的灯杆，P为照明灯.
(1)画出小亮在路灯P照明下的投影，并记作BC.（画图略）
(2)如果小亮身高1.6m，他站在距离灯杆OP为13m的B处时测得其影长BC=2m，求灯杆OP的高度.12m

答案： 解：
(1)如图所示，即为所求.
(2)由题意得 $ OP // AB $，$ OB = 13m $，$ AB = 1.6m $，$ BC = 2m $，则 $ OC = OB + BC = 15m $，
$ \therefore \triangle ABC \backsim \triangle POC $，$ \therefore \frac{AB}{OP} = \frac{BC}{OC} $，即 $ \frac{1.6}{OP} = \frac{2}{15} $，
$ \therefore OP = 12m $.

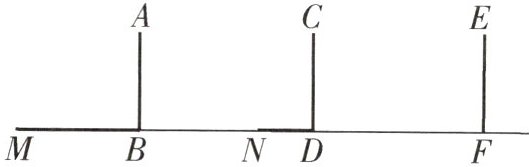
对点训练3 (2024秋·罗湖区校级月考)如图，电线杆上有盏路灯O，小明从点F出发，沿直线FM运动，当他运动2米到达点D处时，测得影长DN=0.6m，再前进2米到达点B处时，测得影长MB=1.6m(图中线段AB，CD，EF表示小明的身高).
(1)请画出路灯O的位置和小明位于F处时，在路灯灯光下的影子；
(2)求小明位于F处的影长.

答案：
解：
(1)如图.

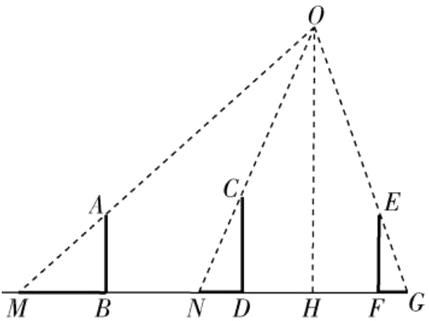
(2)如图，过点 $ O $ 作 $ OH \perp MG $ 于点 $ H $，设 $ DH = xm $，
由 $ AB // CD // OH $，得 $ \frac{MB}{MH} = \frac{ND}{NH} $，
即 $ \frac{1.6}{3.6 + x} = \frac{0.6}{0.6 + x} $，解得 $ x = 1.2 $.
设 $ FG = ym $，同理得 $ \frac{FG}{HG} = \frac{ND}{NH} $，
即 $ \frac{y}{0.8 + y} = \frac{0.6}{1.8} $，解得 $ y = 0.4 $.
所以 $ EF $ 的影长为 $ 0.4m $.

1.（2024秋·龙华区期中）下列哪种影子不是中心投影（A）.
A. 阳光下房屋的影子
B. 晚上在房间内墙上的手影
C. 都市霓虹灯形成的影子
D. 皮影戏中的影子

答案： A

2.（2024·福田区校级模拟）如图，某同学下晚自习后经过一路灯回寝室，他从A处背着灯柱方向走到B处，在这一过程中他在该路灯灯光下的影子（C）.

A. 先变短后变长
B. 由长逐渐变短
C. 由短逐渐变长
D. 始终不变

答案： C

3. 一年级的奇思和爸爸晚上散步，在同一个路灯下，奇思的影子比爸爸的影子长，这时候爸爸和奇思离路灯的距离谁近一点？（B）.
A. 一样
B. 爸爸近一点
C. 奇思近一点
D. 无法比较

答案： B

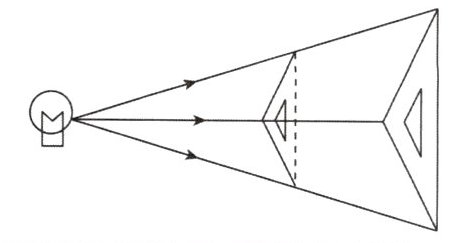
4. 如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为3:5，且三角板的一边长为6cm，则投影三角板的对应边长为10cm.

答案： 10cm