第105页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
1. 手影游戏利用的物理原理是:光是沿直线传播的. 图中小狗手影就是我们小时候常玩的游戏. 在一次游戏中,小明距离墙壁1米,爸爸拿着的光源与小明的距离为2米. 在小明不动的情况下,要使小狗手影的高度增加一倍,则光源与小明的距离应(

A. 减少$\frac {3}{2}$米
B. 增加$\frac {3}{2}$米
C. 减少$\frac {5}{3}$米
D. 增加$\frac {5}{3}$米
A
).
A. 减少$\frac {3}{2}$米
B. 增加$\frac {3}{2}$米
C. 减少$\frac {5}{3}$米
D. 增加$\frac {5}{3}$米
答案:
A
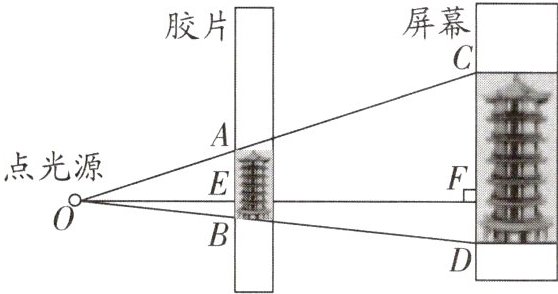
2. (2024秋·宝安区校级期中)如图,点光源O射出的光线沿直线传播,将胶片上的建筑物图片AB投影到与胶片平行的屏幕上,形成影像CD. 已知$AB=0.3dm$,点光源到胶片的距离OE长为6dm,$CD$长为4.3dm,则胶片与屏幕的距离EF为(

A. 86
B. 84
C. 80
D. 78
C
)dm.

A. 86
B. 84
C. 80
D. 78
答案:
C
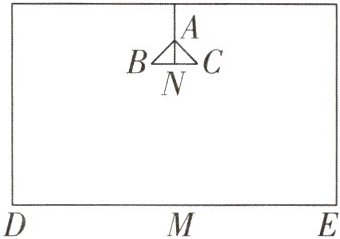
3. 在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡A,为了集中光线,加上了灯罩(如图所示). 已知灯罩深$AN=8cm$,灯泡离地面2m,为了使光线恰好照在墙对角D,E处,灯罩的直径BC应为多少? (结果保留两位小数,$\sqrt {2}\approx 1.414$)

答案:
解:如图,光线恰好照在墙角D,E处,AN = 0.08m,AM = 2 m,
根据题意可知AN⊥BC,
AM⊥DE,
由于房间的地面是边长为4m的正方形,则DE = 4$\sqrt{2}$m.
∵BC//DE,
∴△ABC∽△ADE,
∴$\frac{BC}{DE}$ = $\frac{AN}{AM}$,即$\frac{BC}{4\sqrt{2}}$ = $\frac{0.08}{2}$,
∴BC≈0.23.
答:灯罩的直径BC约为0.23m.

解:如图,光线恰好照在墙角D,E处,AN = 0.08m,AM = 2 m,
根据题意可知AN⊥BC,
AM⊥DE,
由于房间的地面是边长为4m的正方形,则DE = 4$\sqrt{2}$m.
∵BC//DE,
∴△ABC∽△ADE,
∴$\frac{BC}{DE}$ = $\frac{AN}{AM}$,即$\frac{BC}{4\sqrt{2}}$ = $\frac{0.08}{2}$,
∴BC≈0.23.
答:灯罩的直径BC约为0.23m.

4. 某小组的项目式学习活动内容是测量某棵古树的高度AB. 如图,在阳光下,某一时刻,古树AB的影子落在了地上和围墙上,落在地上的长度$BD=21$米,落在墙DC上的长度$DE=1$米,在古树的附近有一棵小树MN,同一时刻,小树的影长$PN=1.8$米,小树的高$MN=1.2$米. 已知点N,P,B,D在一条水平线上,$MN⊥ND,AB⊥ND,ED⊥ND$,请求出该古树的高度AB.


答案:
解:如图,作EF⊥AB于点F,
∵AB⊥ND,ED⊥ND,
∴四边形BDEF是矩形,
∴BF = DE = 1米,EF = BD = 21米.
根据同一时刻的物高与其影长成正比例可得$\frac{MN}{NP}$ = $\frac{AF}{FE}$,
即$\frac{1.2}{1.8}$ = $\frac{AF}{21}$,解得AF = 14,
∴AB = AF + FB = 14 + 1 = 15(米).
答:该古树的高度AB为15米.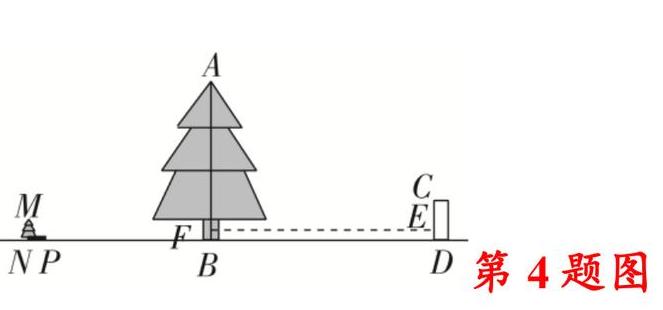
解:如图,作EF⊥AB于点F,
∵AB⊥ND,ED⊥ND,
∴四边形BDEF是矩形,
∴BF = DE = 1米,EF = BD = 21米.
根据同一时刻的物高与其影长成正比例可得$\frac{MN}{NP}$ = $\frac{AF}{FE}$,
即$\frac{1.2}{1.8}$ = $\frac{AF}{21}$,解得AF = 14,
∴AB = AF + FB = 14 + 1 = 15(米).
答:该古树的高度AB为15米.

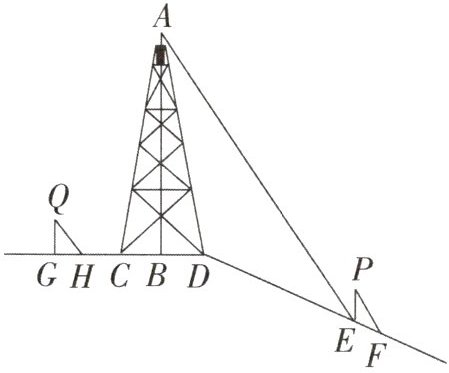
5. 如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的. 在阳光的照射下,塔影DE留在斜坡面上. 在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2m和1m. 已知$CD=12m,DE=18m$,小明和小华的身高均为1.6m,那么塔高AB为多少米?

答案:
解:如图,过点D作DM⊥CD,交AE于点M,过点M作MN⊥AB,垂足为N,则四边形BDMN为矩形,
∴MN = BD,BN = DM.
由题意,得$\frac{DM}{DE}$ = $\frac{1.6}{2}$,
∴DM = DE×1.6÷2 = 14.4(m).
∵MN = BD = $\frac{1}{2}$CD = 6m,$\frac{AN}{MN}$ = $\frac{1.6}{1}$,
∴AN = 1.6×6 = 9.6(m),
∴AB = AN + BN = 9.6 + 14.4 = 24(m).
答:铁塔AB的高度为24m.
解:如图,过点D作DM⊥CD,交AE于点M,过点M作MN⊥AB,垂足为N,则四边形BDMN为矩形,
∴MN = BD,BN = DM.
由题意,得$\frac{DM}{DE}$ = $\frac{1.6}{2}$,
∴DM = DE×1.6÷2 = 14.4(m).
∵MN = BD = $\frac{1}{2}$CD = 6m,$\frac{AN}{MN}$ = $\frac{1.6}{1}$,
∴AN = 1.6×6 = 9.6(m),
∴AB = AN + BN = 9.6 + 14.4 = 24(m).
答:铁塔AB的高度为24m.

查看更多完整答案,请扫码查看


