第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
1. 若点C为线段AB的黄金分割点,且$AC>BC$,则下列各式中不正确的是(
A. $AB:AC=AC:BC$
B. $BC=\frac {3-\sqrt {5}}{2}AB$
C. $AC=\frac {\sqrt {5}+1}{2}AB$
D. $AC\approx 0.618AB$
C
)。A. $AB:AC=AC:BC$
B. $BC=\frac {3-\sqrt {5}}{2}AB$
C. $AC=\frac {\sqrt {5}+1}{2}AB$
D. $AC\approx 0.618AB$
答案:
C
2. 已知线段$AB=2$,点C,D是线段AB上的两个黄金分割点,则CD的长是(
A. $3-\sqrt {5}$
B. $\sqrt {5}$
C. $2\sqrt {5}-4$
D. $\sqrt {5}-1$
C
)。A. $3-\sqrt {5}$
B. $\sqrt {5}$
C. $2\sqrt {5}-4$
D. $\sqrt {5}-1$
答案:
C
3. 当气温与人体正常体温$(37^{\circ }C)$之比等于黄金分割比0.618时,人体感觉最舒适,这个气温约为
23
$^{\circ }C$。(取整数)
答案:
23
4. 我国著名数学家华罗庚曾为普及优选法作出重要贡献。优选法中有一种0.618法应用了(
A. 黄金分割数
B. 平均数
C. 众数
D. 中位数
A
)。A. 黄金分割数
B. 平均数
C. 众数
D. 中位数
答案:
A
5. 如图,校园里一片小小的树叶,P为AB的黄金分割点$(AP>PB)$,如果AB的长度为12cm,求叶柄BP的长度。

解:由黄金分割得$\frac{AP}{AB}=\frac{BP}{AP}$,∴$\frac{12−BP}{12}=\frac{BP}{12−BP}$,整理得$(12−BP)^2=12BP$,解得$BP=$
答:叶柄BP的长度为

解:由黄金分割得$\frac{AP}{AB}=\frac{BP}{AP}$,∴$\frac{12−BP}{12}=\frac{BP}{12−BP}$,整理得$(12−BP)^2=12BP$,解得$BP=$
$18−6\sqrt{5}$
或$BP=18+6\sqrt{5}$(舍去).答:叶柄BP的长度为
$(18−6\sqrt{5})$
cm.
答案:
解:由黄金分割得$\frac{AP}{AB}=\frac{BP}{AP}$,
∴$\frac{12−BP}{12}=\frac{BP}{12−BP}$,整理得$(12−BP)^2=12BP$,解得$BP=18−6\sqrt{5}$或$BP=18+6\sqrt{5}$(舍去).
答:叶柄BP的长度为$(18−6\sqrt{5})$cm.
∴$\frac{12−BP}{12}=\frac{BP}{12−BP}$,整理得$(12−BP)^2=12BP$,解得$BP=18−6\sqrt{5}$或$BP=18+6\sqrt{5}$(舍去).
答:叶柄BP的长度为$(18−6\sqrt{5})$cm.
6. 如图,在$\triangle ABC$中,$AB=AC$,$∠BAC=36^{\circ }$,以点C为圆心,以BC为半径作弧交AC于点D,再分别以B,D为圆心,以大于$\frac {1}{2}BD$的长为半径作弧,两弧相交于点P,作射线CP交AB于点E,连接DE。以下结论不正确的是(
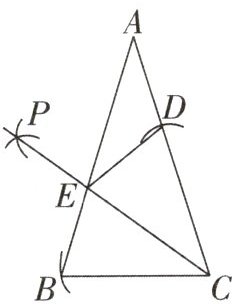
A. $∠BCE=36^{\circ }$
B. $BC=AE$
C. $\frac {BE}{AC}=\frac {\sqrt {5}-1}{2}$
D. $\frac {S_{\triangle AEC}}{S_{\triangle BEC}}=\frac {\sqrt {5}+1}{2}$
C
)。
A. $∠BCE=36^{\circ }$
B. $BC=AE$
C. $\frac {BE}{AC}=\frac {\sqrt {5}-1}{2}$
D. $\frac {S_{\triangle AEC}}{S_{\triangle BEC}}=\frac {\sqrt {5}+1}{2}$
答案:
C 解析:
∵AB=AC,∠BAC=36°,
∴$∠ABC=∠ACB=\frac{180°−∠BAC}{2}=72°$.
由题意得CP平分∠ACB,
∴$∠BCE=∠ACE=\frac{1}{2}∠ACB=36°$,
∴∠A=∠ACE=36°,
∴AE=CE.
∵∠CEB=∠A+∠ACE=72°,
∴∠B=∠CEB=72°,
∴CB=CE,
∴AE=CE=CB.
∵△BCE是顶角为36°的等腰三角形,
∴△BCE是黄金三角形.
∴$\frac{BE}{BC}=\frac{\sqrt{5}−1}{2}$,
∴$\frac{BE}{AE}=\frac{\sqrt{5}−1}{2}$,
∴$\frac{S_{△BCE}}{S_{△AEC}}=\frac{BE}{AE}=\frac{\sqrt{5}−1}{2}$,
∴$\frac{S_{△AEC}}{S_{△BCE}}=\frac{2}{\sqrt{5}−1}=\frac{\sqrt{5}+1}{2}$,
故A,B,D不符合题意,C符合题意. 故选C.
∵AB=AC,∠BAC=36°,
∴$∠ABC=∠ACB=\frac{180°−∠BAC}{2}=72°$.
由题意得CP平分∠ACB,
∴$∠BCE=∠ACE=\frac{1}{2}∠ACB=36°$,
∴∠A=∠ACE=36°,
∴AE=CE.
∵∠CEB=∠A+∠ACE=72°,
∴∠B=∠CEB=72°,
∴CB=CE,
∴AE=CE=CB.
∵△BCE是顶角为36°的等腰三角形,
∴△BCE是黄金三角形.
∴$\frac{BE}{BC}=\frac{\sqrt{5}−1}{2}$,
∴$\frac{BE}{AE}=\frac{\sqrt{5}−1}{2}$,
∴$\frac{S_{△BCE}}{S_{△AEC}}=\frac{BE}{AE}=\frac{\sqrt{5}−1}{2}$,
∴$\frac{S_{△AEC}}{S_{△BCE}}=\frac{2}{\sqrt{5}−1}=\frac{\sqrt{5}+1}{2}$,
故A,B,D不符合题意,C符合题意. 故选C.
7. 古希腊时期,人们认为最美人体的头顶至腰部的长度与腰部至足底的长度之比是黄金分割比。在设计人体雕像时,雕像的腰部以下长为a,身高为b,如果我们选择最美设计方案,当b为2米时,求腰部以下a的长度。$(\sqrt {5}\approx 2.236$,精确到0.01米)
答案:
解:由题意得$\frac{b−a}{a}=\frac{\sqrt{5}−1}{2}$,即$\frac{2−a}{a}=\frac{\sqrt{5}−1}{2}$,解得$a=\sqrt{5}−1≈1.24$(米).
8. 欧几里得的《几何原本》中给出了一个找线段的黄金分割点的方法。如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连接BE,延长DA至点F,使得$EF=BE$,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点。若记正方形AFGH的面积为$S_{1}$,矩形BCIH的面积为$S_{2}$,求$S_{1}$与$S_{2}$的比值。
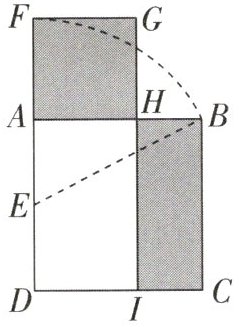
解:∵H是AB的黄金分割点,∴$AH^2=BH·AB$.
∵$S_1=AH^2$,$S_2=BH·BC=BH·AB$,
∴$S_1=S_2$,即$\frac{S_1}{S_2}=$

解:∵H是AB的黄金分割点,∴$AH^2=BH·AB$.
∵$S_1=AH^2$,$S_2=BH·BC=BH·AB$,
∴$S_1=S_2$,即$\frac{S_1}{S_2}=$
1
.
答案:
解:
∵H是AB的黄金分割点,
∴$AH^2=BH·AB$.
∵$S_1=AH^2$,$S_2=BH·BC=BH·AB$,
∴$S_1=S_2$,即$\frac{S_1}{S_2}=1$.
∵H是AB的黄金分割点,
∴$AH^2=BH·AB$.
∵$S_1=AH^2$,$S_2=BH·BC=BH·AB$,
∴$S_1=S_2$,即$\frac{S_1}{S_2}=1$.
查看更多完整答案,请扫码查看


