第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
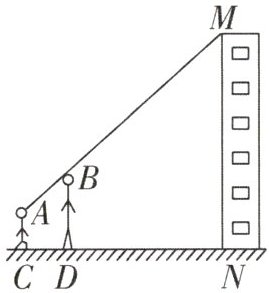
5. 李芳和李亮用如下方法测楼高:如图,李亮蹲在地上,李芳站在李亮和楼之间,当楼的顶部M、李芳的头顶B及李亮的眼睛A恰在一条直线上时,测出CD=1.25 m,DN=30 m(点C,D,N在一条直线上),李芳的身高BD=1.6 m,李亮蹲地观测时眼睛到地面的距离AC=0.8 m.请你根据以上测量数据帮助他们求出楼的高度.

答案:
解:能. 如图,过点 $ A $ 作 $ AF ⊥ MN $,垂足为点 $ F $,交 $ BD $ 于点 $ E $,则 $ NF = DE = AC = 0.8 $ m,$ AE = CD = 1.25 $ m,$ EF = DN = 30 $ m,$ ∠AEB = ∠AFM = 90° $.
∵ $ ∠BAE = ∠MAF $,
∴ $ △ABE \backsim △AMF $.
∴ $ \frac{BE}{MF} = \frac{AE}{AF} $,即 $ \frac{1.6 - 0.8}{MF} = \frac{1.25}{1.25 + 30} $.
∴ $ MF = 20 $.
∴ $ MN = MF + FN = 20 + 0.8 = 20.8 $(m).
答:楼的高度为20.8 m.

解:能. 如图,过点 $ A $ 作 $ AF ⊥ MN $,垂足为点 $ F $,交 $ BD $ 于点 $ E $,则 $ NF = DE = AC = 0.8 $ m,$ AE = CD = 1.25 $ m,$ EF = DN = 30 $ m,$ ∠AEB = ∠AFM = 90° $.
∵ $ ∠BAE = ∠MAF $,
∴ $ △ABE \backsim △AMF $.
∴ $ \frac{BE}{MF} = \frac{AE}{AF} $,即 $ \frac{1.6 - 0.8}{MF} = \frac{1.25}{1.25 + 30} $.
∴ $ MF = 20 $.
∴ $ MN = MF + FN = 20 + 0.8 = 20.8 $(m).
答:楼的高度为20.8 m.

6. (2024秋·龙岗区月考)某校项目式学习小组开展项目活动,过程如下:
项目主题:测量学校旗杆高度
问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,例如自制直角三角形硬纸板,标杆,平面镜,甚至还可以利用无人机,…,确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的部分测量方案:
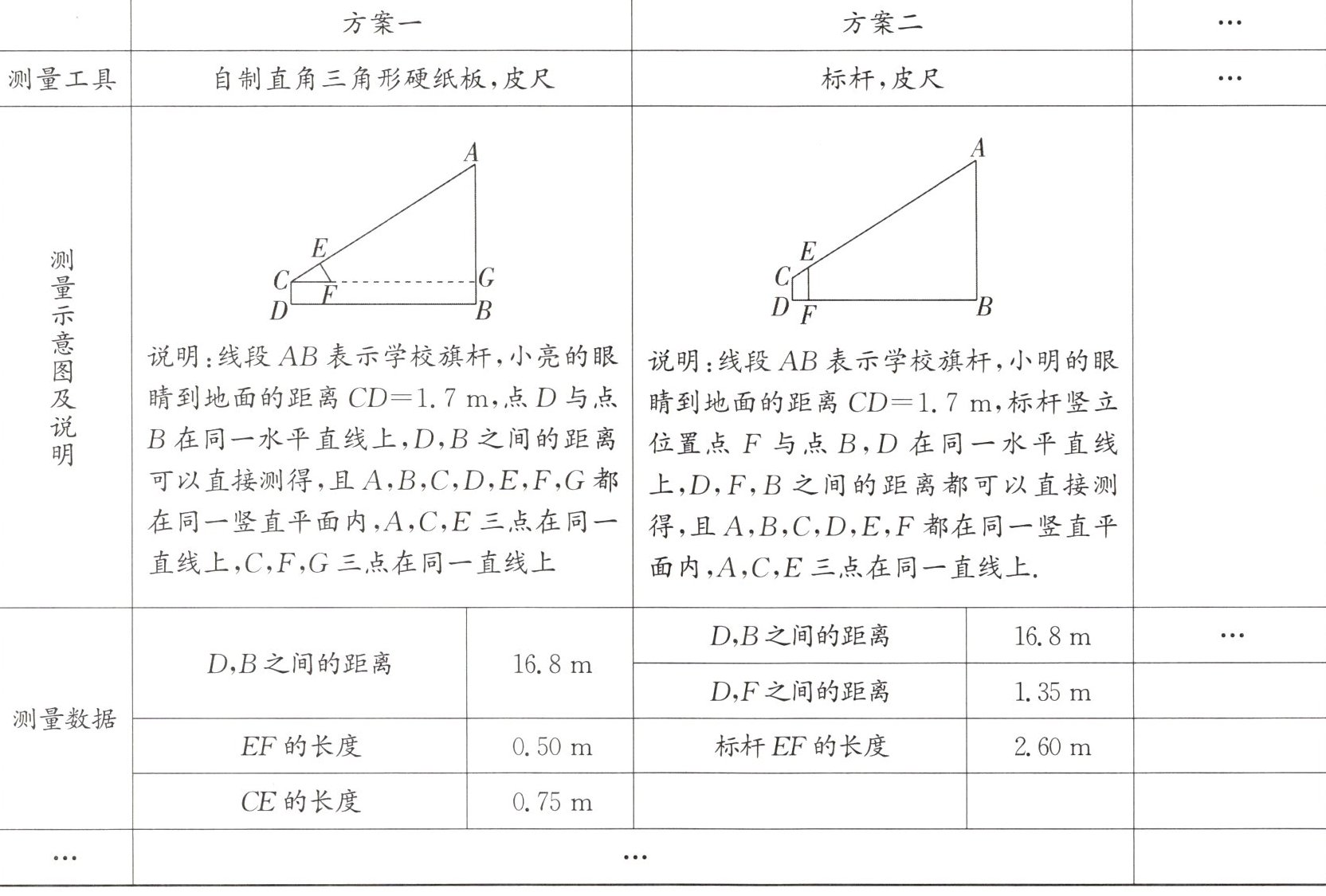
根据上述材料,请你选择一个方案,求出学校旗杆AB的高度.
项目主题:测量学校旗杆高度
问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,例如自制直角三角形硬纸板,标杆,平面镜,甚至还可以利用无人机,…,确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的部分测量方案:

根据上述材料,请你选择一个方案,求出学校旗杆AB的高度.
答案:
解:方案一:由题意得四边形 $ CDBG $ 是矩形,
∴ $ CG = DB = 16.8 $ m,$ CD = GB = 1.7 $ m.
∵ $ ∠ECF = ∠GCA $,$ ∠CEF = ∠CGA = 90° $,
∴ $ △CEF \backsim △CGA $.
∴ $ \frac{CE}{CG} = \frac{EF}{GA} $,
即 $ \frac{0.75}{16.8} = \frac{0.5}{AB - 1.7} $,解得 $ AB = 12.9 $,
答:学校旗杆 $ AB $ 的高度为12.9 m.
方案二:如图,过点 $ C $ 作 $ CH // DB $,交 $ EF $ 于点 $ Q $,交 $ AB $ 于点 $ H $.
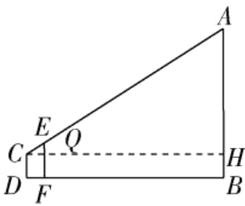
由题意得,四边形 $ CDFQ $ 与四边形 $ CDBH $ 都是矩形,
∴ $ CQ = DF = 1.35 $ m,$ CH = DB = 16.8 $ m,$ CD = QF = HB = 1.7 $ m.
∵ $ EF // AB $,
∴ $ △CEQ \backsim △CAH $,
∴ $ \frac{CQ}{CH} = \frac{EQ}{AH} $,即 $ \frac{1.35}{16.8} = \frac{2.6 - 1.7}{AB - 1.7} $,解得 $ AB = 12.9 $.
答:学校旗杆 $ AB $ 的高度为12.9 m.
解:方案一:由题意得四边形 $ CDBG $ 是矩形,
∴ $ CG = DB = 16.8 $ m,$ CD = GB = 1.7 $ m.
∵ $ ∠ECF = ∠GCA $,$ ∠CEF = ∠CGA = 90° $,
∴ $ △CEF \backsim △CGA $.
∴ $ \frac{CE}{CG} = \frac{EF}{GA} $,
即 $ \frac{0.75}{16.8} = \frac{0.5}{AB - 1.7} $,解得 $ AB = 12.9 $,
答:学校旗杆 $ AB $ 的高度为12.9 m.
方案二:如图,过点 $ C $ 作 $ CH // DB $,交 $ EF $ 于点 $ Q $,交 $ AB $ 于点 $ H $.

由题意得,四边形 $ CDFQ $ 与四边形 $ CDBH $ 都是矩形,
∴ $ CQ = DF = 1.35 $ m,$ CH = DB = 16.8 $ m,$ CD = QF = HB = 1.7 $ m.
∵ $ EF // AB $,
∴ $ △CEQ \backsim △CAH $,
∴ $ \frac{CQ}{CH} = \frac{EQ}{AH} $,即 $ \frac{1.35}{16.8} = \frac{2.6 - 1.7}{AB - 1.7} $,解得 $ AB = 12.9 $.
答:学校旗杆 $ AB $ 的高度为12.9 m.
查看更多完整答案,请扫码查看


