第106页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
6. (2023秋·佛山校级月考)太阳能光伏发电因其清洁、安全、高效等特点,已成为世界各国重点发展的新能源产业. 图1是太阳能电板,图2是其截面示意图,其中GF为太阳能电板,AE,CD均为钢架且垂直于地面DE,AB为水平钢架且垂直于CD,测得$AG=CF=0.4m,BC=0.6m,AC=0.75m$. 若某一时刻的太阳光线垂直照射GF.

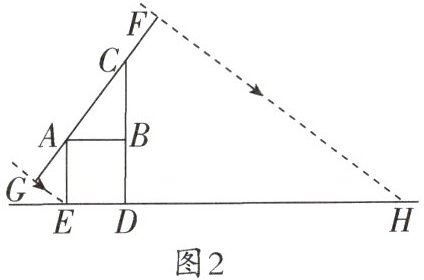
(1)求钢架AE的长;
(2)求太阳能电板GF的影子EH的长(结果保留小数点后两位).


(1)求钢架AE的长;
(2)求太阳能电板GF的影子EH的长(结果保留小数点后两位).
答案:
解:
(1)如图1,由题意,得AE⊥DE,CD⊥DE,AB⊥CD,GE⊥GF,FH⊥GF,
∴∠AED = ∠BDE = ∠ABD = 90°,∠AGE = ∠GFH = 90°,
∴四边形ABDE是矩形,
∴∠BAE = 90°,
∴∠1 + ∠2 = 90°,
又
∵在Rt△AEG中,∠AGE = 90°,
∴∠1 + ∠3 = 90°,
∴∠2 = ∠3.
又
∵∠AGE = ∠ABC = 90°,
∴△AEG∽△CAB,
∴$\frac{AG}{BC}$ = $\frac{AE}{CA}$.
∵AG = 0.4m,BC = 0.6m,AC = 0.75m,
∴$\frac{0.4}{0.6}$ = $\frac{AE}{0.75}$,
∴AE = $\frac{0.4×0.75}{0.6}$ = 0.5(m).
答:钢架AE的长为0.5m.
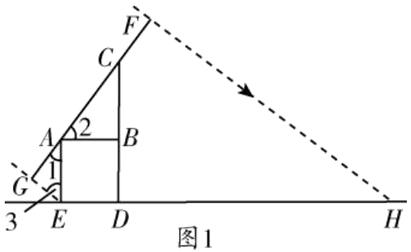
(2)如图2,过点E作EM⊥FH于点M,
∴∠EMF = 90°,
∴∠AGE = ∠GFH = ∠EMF = 90°,
∴四边形EGFM是矩形,
∴∠GEM = 90°,
∴∠3 + ∠4 = 90°.
又
∵∠AED = 90°,
∴∠4 + ∠5 = 90°,
∴∠3 = ∠5.
又
∵∠AGE = ∠EMH = 90°,
∴△AEG∽△HEM,
∴$\frac{AE}{EH}$ = $\frac{EG}{EM}$.
在Rt△AEG中,由勾股定理,得$AE^2 = AG^2 + EG^2$,
∴EG = $\sqrt{AE^2 - AG^2}$ = $\sqrt{0.5^2 - 0.4^2}$ = 0.3(m),
∴EM = GF = AG + AC + CF = 0.4 + 0.75 + 0.4 = 1.55(m),
∴$\frac{0.5}{EH}$ = $\frac{0.3}{1.55}$,
∴EH≈2.58(m).
答:太阳能电板GF的影子EH的长为2.58m.

解:
(1)如图1,由题意,得AE⊥DE,CD⊥DE,AB⊥CD,GE⊥GF,FH⊥GF,
∴∠AED = ∠BDE = ∠ABD = 90°,∠AGE = ∠GFH = 90°,
∴四边形ABDE是矩形,
∴∠BAE = 90°,
∴∠1 + ∠2 = 90°,
又
∵在Rt△AEG中,∠AGE = 90°,
∴∠1 + ∠3 = 90°,
∴∠2 = ∠3.
又
∵∠AGE = ∠ABC = 90°,
∴△AEG∽△CAB,
∴$\frac{AG}{BC}$ = $\frac{AE}{CA}$.
∵AG = 0.4m,BC = 0.6m,AC = 0.75m,
∴$\frac{0.4}{0.6}$ = $\frac{AE}{0.75}$,
∴AE = $\frac{0.4×0.75}{0.6}$ = 0.5(m).
答:钢架AE的长为0.5m.

(2)如图2,过点E作EM⊥FH于点M,
∴∠EMF = 90°,
∴∠AGE = ∠GFH = ∠EMF = 90°,
∴四边形EGFM是矩形,
∴∠GEM = 90°,
∴∠3 + ∠4 = 90°.
又
∵∠AED = 90°,
∴∠4 + ∠5 = 90°,
∴∠3 = ∠5.
又
∵∠AGE = ∠EMH = 90°,
∴△AEG∽△HEM,
∴$\frac{AE}{EH}$ = $\frac{EG}{EM}$.
在Rt△AEG中,由勾股定理,得$AE^2 = AG^2 + EG^2$,
∴EG = $\sqrt{AE^2 - AG^2}$ = $\sqrt{0.5^2 - 0.4^2}$ = 0.3(m),
∴EM = GF = AG + AC + CF = 0.4 + 0.75 + 0.4 = 1.55(m),
∴$\frac{0.5}{EH}$ = $\frac{0.3}{1.55}$,
∴EH≈2.58(m).
答:太阳能电板GF的影子EH的长为2.58m.

7. (2024·凉山州)如图,一块面积为$60cm^{2}$的三角形硬纸板(记为$\triangle ABC$)平行于投影面时,在点光源O的照射下形成的投影是$\triangle A_{1}B_{1}C_{1}$,若$OB:BB_{1}=2:3$,则$\triangle A_{1}B_{1}C_{1}$的面积是(
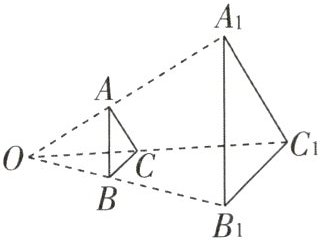
A. $90cm^{2}$
B. $135cm^{2}$
C. $150cm^{2}$
D. $375cm^{2}$
D
).
A. $90cm^{2}$
B. $135cm^{2}$
C. $150cm^{2}$
D. $375cm^{2}$
答案:
D
8. 甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量,下面是他们通过测量得到的一些信息:
甲组:如图1,测得一根直立于平地、长为80cm的竹竿的影长为60cm.
乙组:如图2,测得学校旗杆的影长为900cm.
丙组:如图3,测得校园景观灯(灯罩视为圆柱体,灯杆粗细忽略不计)的灯罩部分影长HQ为90cm,灯杆被阳光照射到的部分PG长为50cm,未被照射到的部分KP长为32cm.
(1)请你根据甲、乙两组得到的信息计算出学校旗杆的高度.
(2)请根据甲、丙两组得到的信息,解答下列问题:
①求灯罩底面半径MK的长;
②正午时刻,太阳刚好直立于头顶,请尝试与丙组同学共同计算出此时灯罩的影子面积.
(1)答:学校旗杆的高度为
(2)①灯罩底面半径MK的长为
②此时灯罩的影子面积为
甲组:如图1,测得一根直立于平地、长为80cm的竹竿的影长为60cm.
乙组:如图2,测得学校旗杆的影长为900cm.
丙组:如图3,测得校园景观灯(灯罩视为圆柱体,灯杆粗细忽略不计)的灯罩部分影长HQ为90cm,灯杆被阳光照射到的部分PG长为50cm,未被照射到的部分KP长为32cm.
(1)请你根据甲、乙两组得到的信息计算出学校旗杆的高度.
(2)请根据甲、丙两组得到的信息,解答下列问题:
①求灯罩底面半径MK的长;
②正午时刻,太阳刚好直立于头顶,请尝试与丙组同学共同计算出此时灯罩的影子面积.
(1)答:学校旗杆的高度为
12m
.(2)①灯罩底面半径MK的长为
24cm
.②此时灯罩的影子面积为
576πcm²
。
答案:
解:
(1)由题意,可知Rt△ABC∽Rt△DEF,
∴$\frac{AB}{DE}$ = $\frac{AC}{DF}$,即$\frac{80}{DE}$ = $\frac{60}{900}$,
∴DE = 1200cm = 12m.
答:学校旗杆的高度为12m.
(2)①根据题意可知,Rt△GPH∽Rt△KPM∽Rt△ABC,
∴$\frac{AC}{GH}$ = $\frac{AB}{PG}$,$\frac{AC}{MK}$ = $\frac{AB}{PK}$,即$\frac{60}{GH}$ = $\frac{80}{50}$,$\frac{60}{MK}$ = $\frac{80}{32}$,
∴GH = 37.5cm,MK = 24cm,
∴灯罩底面半径MK的长为24cm.
②
∵太阳光为平行光,
∴正午时刻灯罩影子为圆形,面积为π×24² = 576π(cm²)。
(1)由题意,可知Rt△ABC∽Rt△DEF,
∴$\frac{AB}{DE}$ = $\frac{AC}{DF}$,即$\frac{80}{DE}$ = $\frac{60}{900}$,
∴DE = 1200cm = 12m.
答:学校旗杆的高度为12m.
(2)①根据题意可知,Rt△GPH∽Rt△KPM∽Rt△ABC,
∴$\frac{AC}{GH}$ = $\frac{AB}{PG}$,$\frac{AC}{MK}$ = $\frac{AB}{PK}$,即$\frac{60}{GH}$ = $\frac{80}{50}$,$\frac{60}{MK}$ = $\frac{80}{32}$,
∴GH = 37.5cm,MK = 24cm,
∴灯罩底面半径MK的长为24cm.
②
∵太阳光为平行光,
∴正午时刻灯罩影子为圆形,面积为π×24² = 576π(cm²)。
查看更多完整答案,请扫码查看


