第166页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
【例3】如图1,某人的一器官后面A处长了一个新生物,现需检测其到皮肤的距离(图1)。为避免伤害器官,可利用一种新型检测技术,检测射线可避开器官从侧面测量。某医疗小组制定方案,通过医疗仪器的测量获得相关数据,并利用数据计算出新生物到皮肤的距离。方案如下:
|示意图|!!|
|----|----|
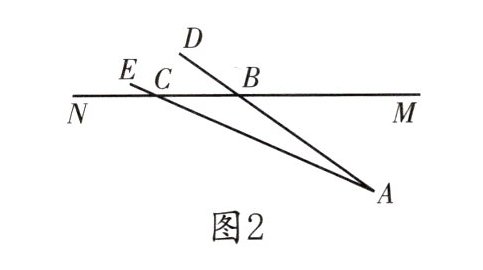
|说明|如图2,新生物在A处,先在皮肤上选择最大限度地避开器官的B处照射新生物,检测射线与皮肤MN的夹角为∠DBN;再在皮肤上选择距离B处9cm的C处照射新生物,检测射线与皮肤MN的夹角为∠ECN。|
|测量数据|∠DBN=35°,∠ECN=22°,BC=9cm。|
请你根据上表中的测量数据,计算新生物A处到皮肤的距离。(结果精确到0.1cm,参考数据:sin 35°≈0.57,cos 35°≈0.82,tan 35°≈0.70,sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.40)
|示意图|!!|
|----|----|
|说明|如图2,新生物在A处,先在皮肤上选择最大限度地避开器官的B处照射新生物,检测射线与皮肤MN的夹角为∠DBN;再在皮肤上选择距离B处9cm的C处照射新生物,检测射线与皮肤MN的夹角为∠ECN。|
|测量数据|∠DBN=35°,∠ECN=22°,BC=9cm。|
请你根据上表中的测量数据,计算新生物A处到皮肤的距离。(结果精确到0.1cm,参考数据:sin 35°≈0.57,cos 35°≈0.82,tan 35°≈0.70,sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.40)

答案:
解:如图,过点A作$AF⊥MN$,垂足为点F.

设$BF=xcm.$
$\because BC=9cm,$
$\therefore CF=BC+BF=(x+9)cm.$
在$Rt△ABF$中,$∠ABF=∠DBN=35^{\circ }.$
$\therefore AF=BF\cdot tan35^{\circ }\approx 0.7xcm.$
在$Rt△ACF$中,$∠ACF=∠ECN=22^{\circ }.$
$\therefore AF=CF\cdot tan22^{\circ }\approx 0.4(x+9)cm.$
$\therefore 0.7x=0.4(x+9),$
解得$x=12.$
$\therefore AF=0.7×12=8.4(cm).$
答:新生物A处到皮肤的距离约为8.4cm.
解:如图,过点A作$AF⊥MN$,垂足为点F.

设$BF=xcm.$
$\because BC=9cm,$
$\therefore CF=BC+BF=(x+9)cm.$
在$Rt△ABF$中,$∠ABF=∠DBN=35^{\circ }.$
$\therefore AF=BF\cdot tan35^{\circ }\approx 0.7xcm.$
在$Rt△ACF$中,$∠ACF=∠ECN=22^{\circ }.$
$\therefore AF=CF\cdot tan22^{\circ }\approx 0.4(x+9)cm.$
$\therefore 0.7x=0.4(x+9),$
解得$x=12.$
$\therefore AF=0.7×12=8.4(cm).$
答:新生物A处到皮肤的距离约为8.4cm.
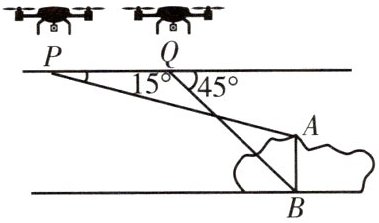
【变式3】某数学兴趣小组用无人机测量奇楼AB的高度,测量方案如图:先将无人机垂直上升至距水平地面225m的点P处,测得奇楼顶端A的俯角为15°,再将无人机沿水平方向飞行200m到达点Q,测得奇楼底端B的俯角为45°。求奇楼AB的高度。(结果精确到1m,参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27)
!
!

答案:
解:如图,延长BA交PQ的延长线于点C,则$∠ACQ=90^{\circ }.$

由题意,得$BC=225m,PQ=200m.$
在$Rt△BCQ$中,$∠BQC=45^{\circ },$
$\therefore CQ=BC=225m.$
$\therefore PC=PQ+CQ=425m.$
在$Rt△PCA$中,$tan∠APC=tan15^{\circ }=\frac {AC}{PC}=\frac {AC}{425}\approx 0.27.$
$\therefore AC\approx 114.75m.$
$\therefore AB=BC-AC\approx 225-114.75=110.25\approx 110(m).$
答:奇楼AB的高度约为110m.
解:如图,延长BA交PQ的延长线于点C,则$∠ACQ=90^{\circ }.$

由题意,得$BC=225m,PQ=200m.$
在$Rt△BCQ$中,$∠BQC=45^{\circ },$
$\therefore CQ=BC=225m.$
$\therefore PC=PQ+CQ=425m.$
在$Rt△PCA$中,$tan∠APC=tan15^{\circ }=\frac {AC}{PC}=\frac {AC}{425}\approx 0.27.$
$\therefore AC\approx 114.75m.$
$\therefore AB=BC-AC\approx 225-114.75=110.25\approx 110(m).$
答:奇楼AB的高度约为110m.
查看更多完整答案,请扫码查看


