2025年世纪金榜高中全程复习方略高中数学A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世纪金榜高中全程复习方略高中数学A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
- 第208页
- 第209页
- 第210页
- 第211页
- 第212页
- 第213页
- 第214页
- 第215页
- 第216页
- 第217页
- 第218页
- 第219页
- 第220页
- 第221页
- 第222页
- 第223页
- 第224页
- 第225页
- 第226页
- 第227页
- 第228页
- 第229页
- 第230页
- 第231页
- 第232页
- 第233页
- 第234页
考点二 应用所给函数模型解决实际问题
[例2](多选题)(2023·新高考Ⅰ卷)噪声污染问题越来越受重视,用声压级来度量声音的强弱,定义声压级$L_{p}=20\times\lg\frac{p}{p_{0}}$,其中常数不妨设$p_{0}$($p_{0}>0$)是听觉下线阈值,$p$是实际声压. 下表为不同声源的声压级:

已知在距离燃油汽车、混合动力汽车、电动汽车10 m处测得实际声压分别为$p_{1},p_{2},p_{3}$,则 ( )
A. $p_{1}\geqslant p_{2}$
B. $p_{2}>10p_{3}$
C. $p_{3}=100p_{0}$
D. $p_{1}\leqslant100p_{2}$
[例2](多选题)(2023·新高考Ⅰ卷)噪声污染问题越来越受重视,用声压级来度量声音的强弱,定义声压级$L_{p}=20\times\lg\frac{p}{p_{0}}$,其中常数不妨设$p_{0}$($p_{0}>0$)是听觉下线阈值,$p$是实际声压. 下表为不同声源的声压级:

已知在距离燃油汽车、混合动力汽车、电动汽车10 m处测得实际声压分别为$p_{1},p_{2},p_{3}$,则 ( )
A. $p_{1}\geqslant p_{2}$
B. $p_{2}>10p_{3}$
C. $p_{3}=100p_{0}$
D. $p_{1}\leqslant100p_{2}$
答案:
ACD 燃油汽车L_p1 = 20×lg$\frac{p_1}{p_0}$∈[60,90],所以$\frac{p_1}{p_0}$=10^($\frac{L_{p_1}}{20}$),L_p1∈[60,90],①同理$\frac{p_2}{p_0}$=10^($\frac{L_{p_2}}{20}$),L_p2∈[50,60],②$\frac{p_3}{p_0}$=10^($\frac{L_{p_3}}{20}$)=10^2 = 100,③对于A,由题表知L_p1≥L_p2,所以A正确;对于B,②÷③得,$\frac{p_2}{p_3}$=10^($\frac{L_{p_2}-L_{p_3}}{20}$)∈[10^($\frac{1}{2}$),10^1],所以$\frac{p_2}{p_3}$≤10,所以B错误;对于C,$\frac{p_3}{p_0}$=10^($\frac{L_{p_3}}{20}$)=10^2 = 100,所以C正确;对于D,①÷②得,$\frac{p_1}{p_2}$=10^($\frac{L_{p_1}-L_{p_2}}{20}$)∈[10^0,10^2],所以$\frac{p_1}{p_2}$∈[1,100],p_1≤100p_2,所以D正确.
对点训练
我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合. 已知某类果蔬的保鲜时间$y$(单位:小时)与储藏温度$x$(单位:℃)满足函数关系$y = e^{ax + b}(a,b$为常数),若该果蔬在6℃的保鲜时间为216小时,在24℃的保鲜时间为8小时,那么在12℃时,该类果蔬的保鲜时间为 ( )
A. 72小时
B. 36小时
C. 24小时
D. 16小时
我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合. 已知某类果蔬的保鲜时间$y$(单位:小时)与储藏温度$x$(单位:℃)满足函数关系$y = e^{ax + b}(a,b$为常数),若该果蔬在6℃的保鲜时间为216小时,在24℃的保鲜时间为8小时,那么在12℃时,该类果蔬的保鲜时间为 ( )
A. 72小时
B. 36小时
C. 24小时
D. 16小时
答案:
A 当x = 6时,e^(6a + b)=216;当x = 24时,e^(24a + b)=8,则$\frac{e^{6a + b}}{e^{24a + b}}$=$\frac{216}{8}$=27,整理可得e^(6a)=$\frac{1}{3}$. 于是e^b = 216×3 = 648,当x = 12时,y = e^(12a + b)=(e^(6a))^2·e^b=$\frac{1}{9}$×648 = 72.
角度1 构造二次函数模型
[例3]如图所示,一直角墙角,两边的长度足够长,在$P$处有一棵树与两墙的距离分别是$a$ m($0 < a < 12$),4 m,不考虑树的粗细,现在用16 m长的篱笆,借助墙角围成一个矩形的花园$ABCD$. 设此矩形花园的面积为$S$ m²,$S$的最大值为$f(a)$,若将这棵树围在花园内,则函数$u = f(a)$的图象大致是 ( )

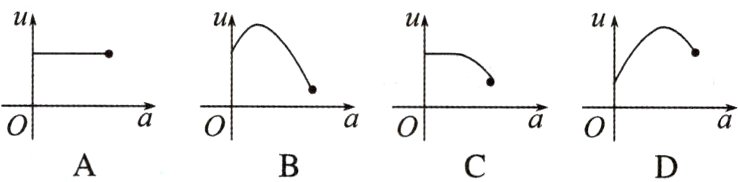
[例3]如图所示,一直角墙角,两边的长度足够长,在$P$处有一棵树与两墙的距离分别是$a$ m($0 < a < 12$),4 m,不考虑树的粗细,现在用16 m长的篱笆,借助墙角围成一个矩形的花园$ABCD$. 设此矩形花园的面积为$S$ m²,$S$的最大值为$f(a)$,若将这棵树围在花园内,则函数$u = f(a)$的图象大致是 ( )


答案:
设AD = x m,则CD=(16 - x)m.要将树围在矩形内,则$\begin{cases}x\geq a\\16 - x\geq4\end{cases}$,所以a≤x≤12.S = x(16 - x)=-(x - 8)^2 + 64,x∈[a,12],若0 < a≤8,则当x = 8时,S_max = 64,若8 < a≤12,则当x = a时,S_max=-a^2 + 16a.综上有f(a)=$\begin{cases}64,0 < a\leq8\\-a^2 + 16a,8 < a\leq12\end{cases}$.
角度2 构造指数函数、对数函数模型
[例4]基本再生数$R_{0}$与世代间隔$T$是某流行性传染病的流行病学基本参数. 基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间. 在该传染病初始阶段,可以用指数模型:$I(t)=e^{rt}$描述累计感染病例数$I(t)$随时间$t$(单位:天)的变化规律,指数增长率$r$与$R_{0}$,$T$近似满足$R_{0}=1 + rT$. 有学者基于已有数据估计出$R_{0}=3.28$,$T = 6$. 据此,在该传染病初始阶段,累计感染病例数增加1倍需要的时间约为($\ln2\approx0.69$) ( )
A. 1.2天
B. 1.8天
C. 2.5天
D. 3.5天
[例4]基本再生数$R_{0}$与世代间隔$T$是某流行性传染病的流行病学基本参数. 基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间. 在该传染病初始阶段,可以用指数模型:$I(t)=e^{rt}$描述累计感染病例数$I(t)$随时间$t$(单位:天)的变化规律,指数增长率$r$与$R_{0}$,$T$近似满足$R_{0}=1 + rT$. 有学者基于已有数据估计出$R_{0}=3.28$,$T = 6$. 据此,在该传染病初始阶段,累计感染病例数增加1倍需要的时间约为($\ln2\approx0.69$) ( )
A. 1.2天
B. 1.8天
C. 2.5天
D. 3.5天
答案:
因为R_0 = 3.28,T = 6,R_0 = 1 + rT,所以r=$\frac{3.28 - 1}{6}$=0.38,所以I(t)=e^(rt)=e^(0.38t).设在该传染病初始阶段,累计感染病例数增加1倍需要的时间为t_1天,则e^(0.38(t + t_1))=2e^(0.38t),所以e^(0.38t_1)=2,所以0.38t_1 = ln 2,所以t_1=$\frac{ln 2}{0.38}$≈$\frac{0.69}{0.38}$≈1.8天.
角度3 构造函数$f(x)=ax+\frac{b}{x}(ab > 0)$模型
[例5]智能辅助驾驶已开始得到初步应用,其自动刹车的工作原理是用雷达测出车辆与障碍物之间的距离,并结合车速转化为所需时间,当此距离等于报警距离时就开始报警,等于危险距离时就自动刹车. 若将报警时间划分为4段,分别为准备时间$t_{0}$与人的反应时间$t_{1}$,系统反应时间$t_{2}$,制动时间$t_{3}$,相应的距离分别为$d_{0},d_{1},d_{2},d_{3}$,如图所示. 当车速为$v$(米/秒),且$0 < v\leqslant33.3$时,通过大数据统计分析得到表中给出的数据(其中系数$k$随地面湿滑程度等路面情况而变化,且$1\leqslant k\leqslant2$).


|阶段|准备|人的反应|系统反应|制动|
| ---- | ---- | ---- | ---- | ---- |
|时间|$t_{0}$|$t_{1}=0.8$秒|$t_{2}=0.2$秒|$t_{3}$|
|距离|$d_{0}=10$米|$d_{1}$|$d_{2}$|$d_{3}=\frac{v^{2}}{20k}$米|
(1)请写出报警距离$d$(米)与车速$v$(米/秒)之间的函数关系式,并求当$k = 2$时,当汽车达到报警距离时,若人和系统均未采取任何制动措施,仍以此速度行驶的情况下,汽车撞上固定障碍物的最短时间;
(2)若要求汽车在$k = 1$的路面上行驶时报警距离均小于50米,则汽车的行驶速度应限制在多少以下(单位:米/秒)?
[例5]智能辅助驾驶已开始得到初步应用,其自动刹车的工作原理是用雷达测出车辆与障碍物之间的距离,并结合车速转化为所需时间,当此距离等于报警距离时就开始报警,等于危险距离时就自动刹车. 若将报警时间划分为4段,分别为准备时间$t_{0}$与人的反应时间$t_{1}$,系统反应时间$t_{2}$,制动时间$t_{3}$,相应的距离分别为$d_{0},d_{1},d_{2},d_{3}$,如图所示. 当车速为$v$(米/秒),且$0 < v\leqslant33.3$时,通过大数据统计分析得到表中给出的数据(其中系数$k$随地面湿滑程度等路面情况而变化,且$1\leqslant k\leqslant2$).


|阶段|准备|人的反应|系统反应|制动|
| ---- | ---- | ---- | ---- | ---- |
|时间|$t_{0}$|$t_{1}=0.8$秒|$t_{2}=0.2$秒|$t_{3}$|
|距离|$d_{0}=10$米|$d_{1}$|$d_{2}$|$d_{3}=\frac{v^{2}}{20k}$米|
(1)请写出报警距离$d$(米)与车速$v$(米/秒)之间的函数关系式,并求当$k = 2$时,当汽车达到报警距离时,若人和系统均未采取任何制动措施,仍以此速度行驶的情况下,汽车撞上固定障碍物的最短时间;
(2)若要求汽车在$k = 1$的路面上行驶时报警距离均小于50米,则汽车的行驶速度应限制在多少以下(单位:米/秒)?
答案:
[解析]
(1)由题意知,d(v)=d_0 + d_1 + d_2 + d_3 = 10 + 0.8v + 0.2v+$\frac{v^2}{20k}$,即d(v)=10 + v+$\frac{v^2}{20k}$,当k = 2时,d(v)=10 + v+$\frac{v^2}{40}$,t(v)=$\frac{d(v)}{v}$=$\frac{10}{v}$+$\frac{v}{40}$+1≥2×$\frac{1}{2}$+1 = 2,当且仅当v = 20时等号成立,0 < v≤33.3,即以此速度行驶的情况下,汽车撞上固定障碍物的最短时间为2秒.
(2)当k = 1时,d(v)<50,即10 + v+$\frac{v^2}{20}$<50,即v^2 + 20v - 800<0,- 40 < v < 20,又0 < v≤33.3,故0 < v < 20,所以汽车的行驶速度应限制在20米/秒以下.
(1)由题意知,d(v)=d_0 + d_1 + d_2 + d_3 = 10 + 0.8v + 0.2v+$\frac{v^2}{20k}$,即d(v)=10 + v+$\frac{v^2}{20k}$,当k = 2时,d(v)=10 + v+$\frac{v^2}{40}$,t(v)=$\frac{d(v)}{v}$=$\frac{10}{v}$+$\frac{v}{40}$+1≥2×$\frac{1}{2}$+1 = 2,当且仅当v = 20时等号成立,0 < v≤33.3,即以此速度行驶的情况下,汽车撞上固定障碍物的最短时间为2秒.
(2)当k = 1时,d(v)<50,即10 + v+$\frac{v^2}{20}$<50,即v^2 + 20v - 800<0,- 40 < v < 20,又0 < v≤33.3,故0 < v < 20,所以汽车的行驶速度应限制在20米/秒以下.
查看更多完整答案,请扫码查看


