《2025年学霸提优大试卷九年级数学全一册苏科版》

14. (12分)如图,已知$△A'B'C'\backsim △ABC$,且$A'E'$、AE 是角平分线,$A'D'$、AD 是中线.求证:$△A'D'E'\backsim △ADE$.

答案：
∵A'D'、AD是两个三角形的中线，A'E'、AE是两条三角形的角平分线，△A'B'C'∽△ABC，
∴$\frac{A'D'}{AD}=\frac{A'B'}{AB}$，$\frac{A'E'}{AE}=\frac{A'B'}{AB}$，∠B'A'C'=∠BAC.
∴$\frac{A'D'}{AD}=\frac{A'E'}{AE}$，∠B'A'E'=$\frac{1}{2}∠B'A'C'=\frac{1}{2}∠BAC=∠BAE$.又
∵△A'B'C'∽△ABC，
∴∠B'=∠B，$\frac{A'B'}{AB}=\frac{B'C'}{BC}$.又
∵点D、点D'分别为BC、B'C'中点，
∴$B'D'=\frac{1}{2}B'C'$，$BD=\frac{1}{2}BC$.
∴$\frac{A'D'}{AD}=\frac{B'C'}{BC}=\frac{A'B'}{AB}$，
∴△A'B'D'∽△ABD，
∴∠B'A'D'=∠BAD，
∴∠D'A'E'=∠DAE，
∴△A'D'E'∽△ADE.

15. (14分)在阳光下,测得一根与地面垂直、长为1米的竹竿的影长为2米.同时两名同学测量一棵树的高度时,发现树的影子不全落在地面上.
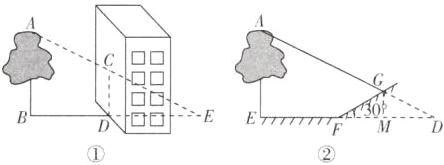
(1)如图①,小明发现树的影子一部分落在地面上,还有一部分影子落在教学楼的墙壁上,量得墙壁上的影长 CD 为 3.5 米,落在地面上的影长 BD 为 6 米,求树 AB 的高度.
(2)如图②,小红发现树的影子恰好落在地面和一斜坡上,此时测得地面上的影长 EF 为 6 米,坡面上的影长 FG 为 4 米.已知斜坡的坡角为$30^{\circ }$,则树的高度为多少米? (结果保留根号)

答案：

(1)如图①，延长AC、BD交于点E，根据物高与影长成正比得$\frac{CD}{DE}=\frac{1}{2}$，
∵$\frac{3.5}{DE}=\frac{1}{2}$，
∴DE=7米，
∴BE=BD+DE=6+7=13(米)，同理$\frac{AB}{BE}=\frac{1}{2}$，
∴$\frac{AB}{13}=\frac{1}{2}$，
∴AB=6.5米.
答：树AB的高度是6.5米.

(2)如图②，延长AG交EF的延长线于点D，过点G作GM⊥DE于点M.在Rt△GFM中，∠GFM=30°，GF=4米，
∴GM=2米，$FM=2\sqrt{3}$米.在Rt△GMD中，
∵同一时刻，长为1米垂直于地面放置的竹竿在地面上的影长为2米，
∴GM:DM=1:2，AE:DE=1:2，
∴DM=4米，
∴$DE=EF+FM+DM=6+2\sqrt{3}+4=(10+2\sqrt{3})$米.在Rt△AED中，$AE=\frac{1}{2}DE=\frac{1}{2}×(10+2\sqrt{3})=(5+\sqrt{3})$米.
答：树的高度是$(5+\sqrt{3})$米.

16. (16分)如图,在菱形 ABCD 中,点 E 在 BC 边上(不与点 B、C 重合),连接 AE、BD 交于点 G.
(1)若$AG= BG,AB= 4,BD= 6$,则线段 DG 的长为$\frac{10}{3}$;
(2)设$BC= kBE,△BGE$的面积为 S,$△AGD$和四边形 CDGE 的面积分别为$S_{1}和S_{2}$,把$S_{1}和S_{2}$分别用含 k、S 的代数式表示;
(3)求$\frac {S_{2}}{S_{1}}$的最大值.$\frac{5}{4}$

答案：
(1)$\frac{10}{3}$[解析]
∵AG=BG，
∴∠BAG=∠ABD.
∵四边形ABCD为菱形，
∴AB=AD，
∴∠ABD=∠ADB，
∴∠BAG=∠ADB，
∴△BAG∽△BDA，
∴$\frac{BA}{BG}=\frac{BD}{BA}$，即$\frac{4}{BG}=\frac{6}{4}$，
∴$BG=\frac{8}{3}$，
∴$DG=BD-BG=6-\frac{8}{3}=\frac{10}{3}$.
(2)
∵四边形ABCD为菱形，
∴BC=AD=kBE，AD//BC.
∵AD//BE，
∴∠DAE=∠BEA，∠ADG=∠EBG，
∴△ADG∽△EBG，
∴$\frac{S_1}{S}=(\frac{AD}{BE})^2=k^2$，$\frac{DG}{BG}=\frac{AD}{BE}=k$，
∴S₁=k²S.
∵$\frac{S_1}{S_{\triangle ABG}}=\frac{DG}{BG}=k$，
∴$S_{\triangle ABG}=\frac{S_1}{k}$.
∵$S_{\triangle ABD}=S_{\triangle BDC}$，
∴$S_2=S_1+\frac{S_1}{k}-S=k^2S+kS-S=(k^2+k-1)S$.
(3)
∵$\frac{S_2}{S_1}=\frac{k^2+k-1}{k^2}=1+\frac{1}{k}-\frac{1}{k^2}=-(\frac{1}{k}-\frac{1}{2})^2+\frac{5}{4}$，
∴最大值为$\frac{5}{4}$.