《2025年学霸提优大试卷九年级数学全一册苏科版》

5. (2023·江西中考)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的$ABC$).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点$A$、$B$、$Q$在同一水平线上,$∠ABC和∠AQP$均为直角,$AP与BC相交于点D$.测得$AB = 40cm$,$BD = 20cm$,$AQ = 12m$,则树高$PQ = $6m.

答案： 5.6　[解析]
∵∠ABC和∠AQP均为直角,
∴BD//PQ,
∴△ABD∽△AQP,
∴$\frac{BD}{PQ}=\frac{AB}{AQ}$.
∵AB=40cm=0.4m,BD=20cm=0.2m,AQ=12m,
∴$PQ=\frac{AQ\cdot BD}{AB}=\frac{12×0.2}{0.4}=6(m)$.

6. (2023·镇江中考)《九章算术》中记载:“今有勾八步,股一十五步.问勾中容圆,径几何?”译文:现在有一个直角三角形,短直角边的长为8步,长直角边的长为15步.问这个直角三角形内切圆的直径是多少?书中给出的算法译文如下:如图,根据短直角边的长和长直角边的长,求得斜边的长.用直角三角形三条边的长相加作为除数,用两条直角边相乘的积再乘2作为被除数,计算所得的商就是这个直角三角形内切圆的直径.根据以上方法,求得该直径等于6步.(注:“步”为长度单位)
 

答案： 6.6　[解析]根据题意，由勾股定理计算得斜边为$\sqrt{8^{2}+15^{2}}=17$(步)，则该直角三角形内切圆的直径为$\frac{2×8×15}{8+15+17}=6$(步).

7. (2023·东营中考)《九章算术》是中国传统数学重要的著作之一,其中第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用几何语言表达为:如图,$AB是\odot O$的直径,弦$CD \perp AB于点E$,$EB = 1$寸,$CD = 10$寸,则直径$AB$长为26寸.

答案： 7.26　[解析]
∵弦CD⊥AB,AB为⊙O的直径,
∴E为CD的中点.又
∵CD=10寸,
∴$CE=DE=\frac{1}{2}CD=5$寸.设OC=OA=x寸,则AB=2x寸,OE=(x - 1)寸,由勾股定理得$OE^{2}+CE^{2}=OC^{2}$,即$(x - 1)^{2}+5^{2}=x^{2}$,解得x=13,
∴AB=26寸.

8. (2023·常德中考)沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,$\overset{\frown}{AB}是以O$为圆心,$OA$长为半径的圆弧,$C是弦AB$的中点,$D在\overset{\frown}{AB}$上,$CD \perp AB$.“会圆术”给出$\overset{\frown}{AB}长l的近似值s$的计算公式:$s = AB + \frac{CD^{2}}{OA}$,当$OA = 2$,$∠AOB = 90^{\circ}$时,$|l - s| = $0.1.(结果保留一位小数)

答案： 8.0.1　[解析]
∵OA=OB=2,∠AOB=90°,
∴$AB=2\sqrt{2}$.
∵C是弦AB的中点,D在$\overset{\frown}{AB}$上,CD⊥AB,
∴如图,延长DC可得点O在直线DC上,$OC=\frac{1}{2}AB=\sqrt{2}$,
∴$CD=OD - OC=2-\sqrt{2}$,
∴$s=AB+\frac{CD^{2}}{OA}=2\sqrt{2}+\frac{(2-\sqrt{2})^{2}}{2}=3$,$l=\frac{90×2×2\pi}{360}=\pi$,
∴|l - s|=|π - 3|≈0.1.

9. (2023·黄冈中考)如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中$AF = a$,$DF = b$,连接$AE$、$BE$,若$\triangle ADE与\triangle BEH$的面积相等,则$\frac{b^{2}}{a^{2}} + \frac{a^{2}}{b^{2}} = $3.

答案： 9.3　[解析]
∵AF=a,DF=b,
∴ED=AF=a,EH=EF=DF - DE=b - a.
∵△ADE与△BEH的面积相等,
∴$\frac{1}{2}DE\cdot AF=\frac{1}{2}EH\cdot BH$,
∴$\frac{1}{2}a\cdot a=\frac{1}{2}(b - a)\cdot b$,
∴$a^{2}=b^{2}-ab$,
∴$1=(\frac{b}{a})^{2}-\frac{b}{a}$,
∴$(\frac{b}{a})^{2}-\frac{b}{a}-1=0$,解得$\frac{b}{a}=\frac{\sqrt{5}+1}{2}$(负值已舍去),
∴$\frac{b^{2}}{a^{2}}+\frac{a^{2}}{b^{2}}=(\frac{\sqrt{5}+1}{2})^{2}+(\frac{2}{\sqrt{5}+1})^{2}=3$.

10. (2024·甘肃中考)马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.如图①的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图②,已知$\odot O和圆上一点M$.作法如下:
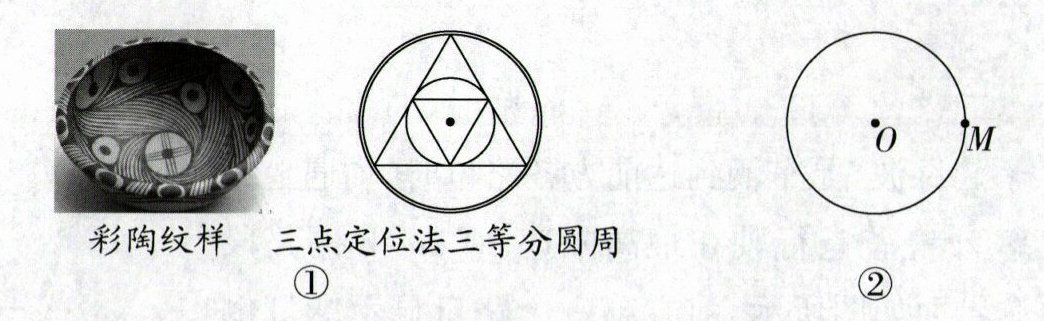
①以点$M$为圆心,$OM$长为半径,作弧交$\odot O于A$,$B$两点;
②延长$MO交\odot O于点C$;
即点$A$、$B$、$C将\odot O$的圆周三等分.
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图②中将$\odot O$的圆周三等分(保留作图痕迹,不写作法);
(2)根据(1)中画出的图形,连接$AB$、$AC$、$BC$,若$\odot O的半径为2cm$,则$\triangle ABC$的周长为______cm.

答案：
10.
(1)根据基本作图的步骤,作图如图①所示.
则点A、B、C是求作的⊙O的圆周三等分点
　　　　　
(2)$6\sqrt{3}$　[解析]如图②,连接AC、BC、AB、AM,设AB、OM的交点为D,根据垂径定理得到AD⊥OM,
∵⊙O的半径为2cm,MC是直径,△ABC是等边三角形,
∴∠CAM=90°,∠CMA=∠B=60°,MC=4cm,
∴$AC=MC\sin\angle CMA=\sin60^{\circ}×4=2\sqrt{3}(cm)$,
∴△ABC的周长为$AB + BC + AC=6\sqrt{3}(cm)$.