《2025年学霸提优大试卷九年级数学全一册苏科版》

1. (2024·牡丹江中考)小明同学手中有一张矩形纸片 $ABCD$,$AD = 12\ \text{cm}$,$CD = 10\ \text{cm}$,他进行了如下操作：
第一步,如图①,将矩形纸片对折,使 $AD$ 与 $BC$ 重合,得到折痕 $MN$,将纸片展平。
第二步,如图②,再一次折叠纸片,把 $\triangle ADN$ 沿 $AN$ 折叠得到 $\triangle AD'N$,$AD'$ 交折痕 $MN$ 于点 $E$,则线段 $EN$ 的长为 (B)
A.$8\ \text{cm}$
B.$\frac{169}{24}\ \text{cm}$
C.$\frac{167}{24}\ \text{cm}$
D.$\frac{55}{8}\ \text{cm}$

答案： B 【解析】
∵ 四边形ABCD是矩形，
∴ AB=CD=10 cm，由折叠可得AM=$\frac{1}{2}$AB=5 cm，AD=AD'=12 cm، MN⊥AB，∠DAN=∠D'AN，
∴ 四边形AMND是矩形，
∴ MN//AD，MN=AD=12 cm，
∴ ∠DAN=∠ANM，
∴ ∠ANM=∠D'AN，
∴ EA=EN.设EA=EN=x cm，则EM=(12 - x)cm，在Rt△AME中，根据勾股定理可得AM²+ME²=AE²，即5²+(12 - x)²=x²，解得x=$\frac{169}{24}$，即EN=$\frac{169}{24}$cm，故选B.

2. (2024·宜宾中考)如图,一个圆柱形容器,其底部有三个完全相同的小孔槽,分别命名为甲槽、乙槽、丙槽。有大小质地完全相同的三个小球,每个小球标有从 $1$ 至 $9$ 中选取的一个数字,且每个小球所标数字互不相同。作如下操作：将这三个小球放入容器中,摇动容器使这三个小球全部落入不同的小孔槽(每个小孔槽只能容下一个小球),取出小球记录下各小孔槽的计分(分数为落入该小孔槽小球上所标的数字),完成第一次操作,再重复以上操作两次。已知甲槽、乙槽、丙槽三次操作计分之和分别为 $20$ 分、$10$ 分、$9$ 分,其中第一次操作计分最高的是乙槽,则第二次操作计分最低的是______。(从“甲槽”“乙槽”“丙槽”中选填)


乙槽

答案： 乙槽 【解析】设第一次操作乙得x分，第二次操作乙得y分，第三次操作乙得z分，根据题意，得x + y + z = 10，当y = z = 1时，x最大，为8，根据每次操作数字不相同，故数字1不可能再出现，故第二次操作计分最低的是乙槽.

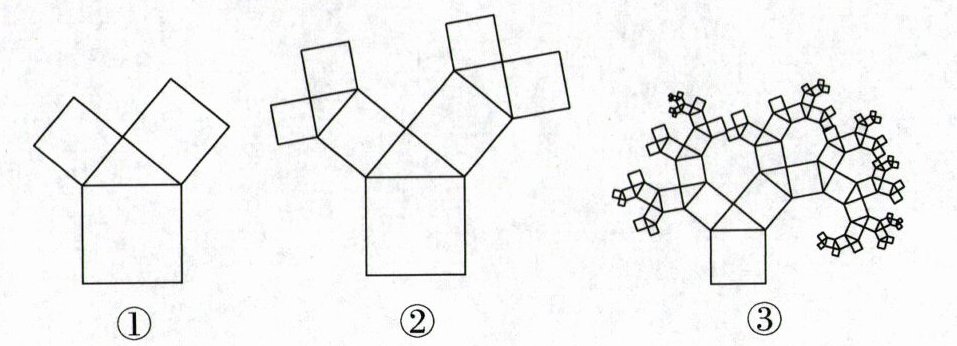
3. (2024·大庆中考)如图①,直角三角形的两个锐角分别是 $40^{\circ}$ 和 $50^{\circ}$,其三边上分别有一个正方形。执行下面的操作：由两个小正方形向外分别作锐角为 $40^{\circ}$ 和 $50^{\circ}$ 的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形,图②是 $1$ 次操作后的图形,图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”。若图①中的直角三角形斜边长为 $2$,则 $10$ 次操作后图形中所有正方形的面积和为______。

答案：
48 【解析】如图①，
∵ ∠ACB = 90°，根据勾股定理得，AC²+BC²=AB²=2²=4，
∴ 图①中所有正方形面积和为4 + 4 = 8，图②中所有正方形面积和，即1次操作后的图形中所有正方形的面积和为8 + 4 = 12，2次操作后的图形中所有正方形的面积和为8 + 4×2 = 16……
∴ n次操作后的图形中所有正方形的面积和为8 + 4n，
∴ 10次操作后的图形中所有正方形的面积和为8 + 4×10 = 48.