《2025年重点中学招生分班五年真题分类卷数学》

1. (2024重庆 BSBB 中学)$a^{m}$表示 m 个 a 连续相乘,那么$2^{2020}+3^{2021}+4^{2022}+5^{2023}+6^{2024}$结果的个位数字是6。

答案： 6 【解析】因为 $2^{1}=2,2^{2}=4,2^{3}=8,2^{4}=16,2^{5}=32$, $2020÷4=505$,所以 $2^{2020}$ 的个位数字是 6,因为 $3^{1}=3,3^{2}=9,3^{3}=27,3^{4}=81,3^{5}=243,2021÷4=505\cdots\cdots1$,所以 $3^{2021}$ 的个位数字是 3,$4^{1}=4,4^{2}=16,4^{3}=64$, $2022÷2=1011$,所以 $4^{2022}$ 的个位是 6,$5^{1}=5,5^{2}=25$,所以 $5^{2023}$ 的个位是 5,$6^{1}=6,6^{2}=36$,所以 $6^{2024}$ 的个位是 6,6+3+6+5+6=26。

2. (2023陕西 GX3C 创新班)在乘积$1×2×3×... ×498×499×500$中,末尾有124个零。

答案： 124 【解析】有因数 5 的个数是:500÷5=100,有因数 25 的个数为:500÷25=20,有因数 125 的个数为:500÷125=4,所以一共有:100+20+4=124(个)。

3. (2024陕西 JDFZ 少年班)$1^{8}+2^{8}+3^{8}+4^{8}+5^{8}+6^{8}+7^{8}+8^{8}+9^{8}+10^{8}+11^{8}$的个位数字是4。

答案： 4 【解析】因为 1 的任何次方都是 1,所以 $1^{8}$ 的个位是 1。$2^{8}=(2×2×2×2)×(2×2×2×2)=16^{2}$,个位是 6。像这样每 4 个数一组的分组,可以更快得到数字的 8 次方的尾数,如 $3^{8}=(3×3×3×3)×(3×3×3×3)=81^{2}$,个位是 1,$4^{8}$ 的个位是 6,$5^{8}$ 的个位是 5,$6^{8}$ 的个位是 6,$7^{8}$ 的个位是 1,$8^{8}$ 的个位是 6,$9^{8}$ 的个位是 1,$10^{8}$ 的个位是 0,$11^{8}$ 的个位是 1。1+6+1+6+5+6+1+6+1+0+1=34,因此,$1^{8}+2^{8}+3^{8}+4^{8}+5^{8}+6^{8}+7^{8}+8^{8}+9^{8}+10^{8}+11^{8}$ 的个位数字是 4。

4. (2024陕西 JDFZ 少年班)算式$7+7×7+7×7×7+... +7×7×... ×7$计算结果的末两位数字是99。
31个7

答案： 99 【解析】7 除以 100 的余数为 7,7×7 除以 100 的余数为 49,7×7×7 除以 100 的余数为 43,7×7×7×7 除以 100 的余数为 1,7×7×7×7×7 除以 100 的余数为 7,…,则 7+7×7+…+7×7×…×7(31个7)除以 100 所得的余数,4 个数一循环,依次为 7,49,43,1。31÷4=7……3,所以算式 7+7×7+…+7×7×…×7(31个7)计算结果除以 100 的余数是[(7+49+43+1)×7+7+49+43]÷100=799÷100=7……99。所以算式计算结果的末两位数字是 99。

5. (2024陕西 GXYZ 博雅班)图中是一行按规律排列的图形,第 288 个图形是△。
□ ○ △ ◇ ♦ □ ○ △ ◇ ♦ □ ○ ...

答案： △

6. (2023陕西 GXYZSY 中学)如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2020 将与圆周上数字2重合。

答案： 2

7. (2024河南 ZZ 中学)如果四个小朋友站成一排,老师按图中所示的规则数数,数到 2022 时对应的小朋友可得一朵红花。那么,得红花的小朋友是______。

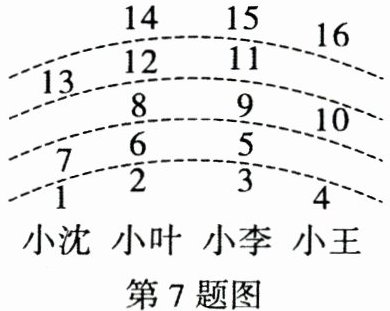
小叶

答案： 小叶

8. (2024陕西 GXYZSY 中学)$2\frac {3}{7}$用循环小数表示,小数点后第 2014 位上的数字是5。

答案： 5 【解析】$2\frac{3}{7}=2.\dot{4}2857\dot{1}$,循环节由 6 个数字组成,2014÷6=335(组)……4(个),也就是说小数点后 2014 位里面含有 335 组这样的循环节,剩余的 4 个数字是第 336 组的前 4 位,即第 2014 位上的数字是循环节第 4 个数字 5。

9. (2024陕西 GXYZ 博班)$2^{2023}$除以 33 的余数为8。

答案： 8 【解析】$2^{1}÷33$ 余 2,$2^{2}÷33$ 余 4,$2^{3}÷33$ 余 8,$2^{4}÷33$ 余 16,$2^{5}÷33$ 余 32,$2^{6}÷33$ 余 31,$2^{7}÷33$ 余 29,$2^{8}÷33$ 余 25,$2^{9}÷33$ 余 17,$2^{10}÷33$ 余 1,$2^{11}÷33$ 余 2,$2^{12}÷33$ 余 4,$2^{13}÷33$ 余 8,…,余数以 10 个为一周期循环,2023÷10 余 3,则 $2^{2023}÷33$ 余数为 8。

10. (2024陕西 XA1Z 少年班)如图,两个连续在一起的菱形的边长都是1 cm,一只电子甲虫从点A开始按 ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行 2018 cm 时停下,则它停的位置是______C。

答案： C 【解析】因为两个菱形的边长都为 1 cm,所以从 A 开始移动 8 cm 后回到点 A,2018÷8=252……2,即移动 2018 cm 为第 253 个循环组的第 2 cm,在点 C 处。

11. (2020陕西 GXYZ)如图,电子跳蚤每跳1步,可从1个圆圈跳到相邻的圆圈。现在,1只红跳蚤从标有数字“0”的圆圈按顺时针方向跳了1997步,落在1个圆圈里,1只黑跳蚤也从标有数字“0”的圆圈起跳,但是它是沿着逆时针方向跳了2015步,落在另一个圆圈里。问:这两个圆圈里数字的乘积是______。

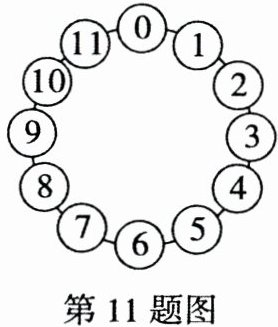
5

答案： 5 【解析】根据题意可知,0,1,2,3,…,11 即 12 个数为一次循环。因为 1997÷12=166……5,所以红跳蚤按顺时针方向跳完后落在的圆圈里的数字为 5;因为 2015÷12=167……11,所以黑跳蚤按逆时针方向跳完后落在的圆圈里的数字为 1,所以这两个圆圈里的数字的乘积是 5×1=5。