《2025年重点中学招生分班五年真题分类卷数学》

1. (2023 陕西 GX3C 创新班)如图是某城市局部街道示意图,某人想从街道口 A 到街道口 B,要使走的路程最短,不同的走法有(C)种。

A.8
B.9
C.10
D.11

答案： C

2. (2024 重庆 NY 中学)一把钥匙只能开一把锁。现在有 5 把钥匙 5 把锁,但不知哪把钥匙开哪把锁,若使全部的钥匙和锁相匹配,试开的次数最多是10次。

答案： 10

3. (2024 重庆 8Z)每次从 3,4,5,10,12,21 中任取两个数,可以组成8个最简真分数。

答案： 8 【解析】3作分母0个满足要求，4作分母$\frac{3}{4}$一个满足要求，5作分母$\frac{3}{5}$、$\frac{4}{5}$两个满足要求，10作分母$\frac{3}{10}$一个满足要求，12作分母$\frac{5}{12}$一个满足要求，21作分母$\frac{4}{21}$、$\frac{5}{21}$、$\frac{10}{21}$三个满足要求，共$0 + 1 + 2 + 1 + 1 + 3 = 8$ (个)。

4. (2023 陕西 JDFZ 少年班)今有长度分别为 1 厘米、2 厘米、3 厘米、……、9 厘米长的木棍各一根(规定不许折断),从中选用若干根组成正方形,可有9种不同的方法。

答案： 9 【解析】根据题意分析可得，利用题干中的小棒可组成的正方形有：①边长是11厘米的正方形1种，边长分别为：$9 + 2$，$8 + 3$，$7 + 4$，$6 + 5$；②边长是10厘米的正方形1种，边长分别为：$9 + 1$，$8 + 2$，$7 + 3$，$6 + 4$；③边长是9厘米的正方形5种，边长分别为：9，$8 + 1$，$7 + 2$，$6 + 3$；9，$8 + 1$，$7 + 2$，$5 + 4$；9，$8 + 1$，$6 + 3$，$5 + 4$；9，$7 + 2$，$6 + 3$，$5 + 4$；$8 + 1$，$7 + 2$，$6 + 3$，$5 + 4$；④边长是8厘米的正方形1种，边长分别为：8，$7 + 1$，$6 + 2$，$5 + 3$；⑤边长是7厘米的正方形1种，边长分别为：7，$6 + 1$，$5 + 2$，$4 + 3$。边长小于等于6时，不能凑够四条正方形的边长，能拼出的正方形只有边长为7厘米，8厘米，9厘米，10厘米，11厘米，总共有$1 + 1 + 5 + 1 + 1 = 9$ (种)不同方法。

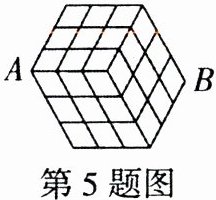
5. (2024 重庆 LJBS 中学)如图为某街区平面图,相邻两点间连线的长度均为 1,甲从 A 地出发去 B 地,乙从 B 地出发去 A 地,两人同时出发,沿格线走最短路径到达目的地,如果乙的速度为甲的 2 倍,那么两人会在途中相遇的路线共有______种。

答案：
5100 【解析】A、B两地间的最短路线长度为9，由于乙的速度是甲的2倍，所以相遇时甲走3，乙走6，相遇点只能在如解图的C，D，E，F，G，H，I这7个点。可分成以下情况：①若在点C相遇，从A到C的最短路线共有1条，从C到B的最短路线共有1条，所以甲经过C的最短路线共$1×1 = 1$ (条)，同理乙经过C的最短路线也是1条，那么在点C相遇共$1×1 = 1$ (种)；②若在点D相遇，从A到D的最短路线共有3条，从D到B的最短路线共有6条，所以甲经过D的最短路线共$3×6 = 18$ (条)，同理乙经过D的最短路线也是18条，那么在点D相遇共$18×18 = 324$ (种)；③若在点E相遇，从A到E的最短路线共有3条，从E到B的最短路线共有15条，所以甲经过E的最短路线共$3×15 = 45$ (条)，同理乙经过E的最短路线也是45条，那么在点E相遇共$45×45 = 2025$ (种)；④若在点F相遇，从A到F的最短路线共有1条，从F到B的最短路线共有20条，所以甲经过F的最短路线共$1×20 = 20$ (条)，同理乙经过F的最短路线也是20条，那么在点F相遇共$20×20 = 400$ (种)；⑤在点G相遇与③相同，共有2025种；⑥在点H相遇与②相同，共有324种；⑦在点I相遇与①相同，共有1种。综上，两人会在途中相遇的路线共有$1 + 324 + 2025 + 400 + 2025 + 324 + 1 = 5100$ (种)。

6. (2023 陕西 TYZ)一些数字可以颠倒过来看,例如 0,1,8 颠倒过来还是本身,6 颠倒过来是 9,9 颠倒过来是 6,其他数字颠倒过来都不构成数字。类似的,一些多位数也可以颠倒过来看,比如 106 颠倒过来是 901。假设某个城市的车牌只由 3 位数字组成,每一位都可以取 0 到 9。请问这个城市最多有______个车牌颠倒过来恰好还是原来的车牌。
15

答案： 15 【解析】颠倒后不变的：①两端都为0有000，010，080共3种情况；②两端都为1有101，111，181共3种情况；③两端都为8的有808，818，888共3种情况；④两端为6和9的有609，906，619，916，689，986共6种情况，所以一共有$3 + 3 + 3 + 6 = 15$ (个)车牌倒过来恰好还是原来的车牌。

7. (2024 陕西 GDFZ 丘成桐班)若把英语单词 matter 中的字母顺序写错了,则可能出现的错误共有359种。

答案： 359 【解析】把英语单词“matter”的字母顺序写错了，“matter”有6个字母，所以排法有$6×5×4×3×2×1 = 720$ (种)，因为有两个t重复，总数要除以2，可能出现的错误种数再减去1种正确的，所以可能出现的错误共有$720÷2 - 1 = 359$ (种)。

8. (2024 陕西 GXYZ 博雅班)有 1 名老师和 6 名获奖学生排成一排照相留念,则老师不站两端的不同排法有3600种。

答案： 3600

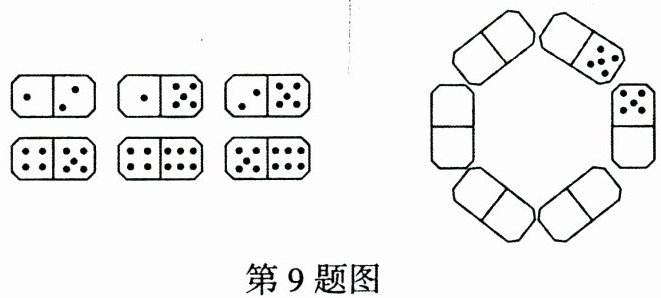
9. (2023 陕西 CXJDGZ)如图,有六张多米诺骨牌,每张牌都由两个区域构成,每个区域上都标有 1~6 的点数,现在要将这六张牌围成一圈,要求相邻两张牌的对应区域点数相同。如右图所示,已经给出了两张牌的某个区域的点数,那么,有______种不同的方法。

答案：
8 【解析】由题图知：六张多米诺骨牌的点数分别是1 - 2，1 - 5，2 - 5，4 - 5，4 - 6，5 - 6，要求相邻两张牌的对应区域点数相同，能连着串出两串数，①$5 - 1⇔1 - 2⇔2 - 5$；②$5 - 6⇔6 - 4⇔4 - 5$ (每串数字的方向也可以反过来)如解图所示，整个一圈可以分为两个部分，一个部分正好放一串数，由于题目已经规定两个5的位置，所以与分割线接近的四个位置都放5，所以位置1有4个数可以选择(1，2，4，6)，一旦确定了，一串数就用了位置2所在的半圈：第一种情况：如果位置1所在的半圈用了①串数，位置2所在的半圈只能用②串数，位置2有两个数可以选择(6，4)；第二种情况：如果位置1所在的半圈用了②串数，位置2所在的半圈只能用①串数，位置2有两个数可以选择(1，2)，所以位置2有2个数可以选择，根据乘法原理，有$4×2 = 8$ (种)不同的方法。

10. (2024 陕西 JDFZ 少年班)一种电子表在 6 时 24 分 30 秒显示 6:24:30,那么从 8 时到 9 时这段时间里,此表的 5 个数字都不相同的时刻一共有1260个。

答案： 1260 【解析】设$A:BC:DE$是满足题意的时刻，则A为8，B、D应从0，1，2，3，4，5这6个数字中任意选择两个不同的数字，所以有$6×5 = 30$ (种)选法，而C、E应从剩下的7个数字中任意选择两个不同的数字，所以有$7×6 = 42$ (种)选法，所以共有$30×42 = 1260$ (种)选法，即都不相同的时刻一共有1260个。

11. (2024 陕西 JDFZ)甲、乙、丙三人相约一起去做核酸检测,到达检测点后,发现有 A,B 两支正在等待检测的队伍,则甲、乙、丙三人不同的排队方案共有24种。

答案： 24 【解析】对该问题进行分类，分成以下情况：①3人都到A队伍检测，排队方案有$3×2×1 = 6$ (种)；②2人到A队伍检测，排队方案有$3×2 = 6$ (种)；③1人到A队伍检测，两人在B队排队，排队方案有$3×2 = 6$ (种)；④0人到A队伍检测，3人在B队排队，排队方案有$3×2×1 = 6$ (种)，一共有$6 + 6 + 6 + 6 = 24$ (种)。

12. (2024 重庆 LJBS 学校)在一个国家竞赛联盟中有 16 支曲棍球队,它们被分成两组,每组 8 队。在一个赛季中,每支球队要同本组中其他每支球队打一场球,然后同另一组中的所有球队各打一场球,最后再同本组中其他球队各打一场球,那么,在这个赛季中共进行了______场比赛。
120

答案： 120

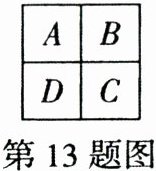
13. (2023 陕西 TYZ)如图,在一个田字形的区域 A,B,C,D 栽种观赏植物,要求同一个区域中种同一种植物,相邻的两块种不同的植物,现有 3 种不同的植物可供选择,那么共有18种不同的栽种方案。

答案： 18 【解析】当A，C种同一种植物时，A，C有3种选择方案，则B与D各有2种选择方案，此时有$3×2×2 = 12$ (种)选择方案；当A，C种植不同植物时，A有3种选择方案，C有2种选择方案，B与D各有1种选择方案，此时有$3×2×1×1 = 6$ (种)选择方案，故一共有$12 + 6 = 18$ (种)不同的栽种方案。