《2025年重点中学招生分班五年真题分类卷数学》

14. (2022 陕西 JDFZ)小军在计算$68×(☆+2)$时把算式抄成$68×☆+2$,正确结果与这样计算的结果相差134

答案： 134

15. (2023 陕西 GDFZ 改编)小李同学漏看了写在两个三位数之间的乘号,将其当成了一个六位数,该六位数刚好是原来乘积的 7 倍,则这两个三位数分别是143和143

答案： 143　143　[解析]设这两个三位数分别是$x$和$y$，由题意得$1000x + y = 7xy$，等式两边同时除以$x$，则$1000+\frac{y}{x}=7y$，$\frac{y}{x}=7y - 1000$，$0＜7y - 1000＜10$，$142＜y＜145$，$y$取144、143两个整数值，当$y = 144$时，$x = 18$，不符合题意，所以$y = 143$，$7y-1000 = 1$，所以$x = 143$，所以此六位数为143143，所以这两个三位数分别是143和143。

16. (2024 陕西 GXYZ 博雅班)一本书有 500 页,编上页码 1、2、3、4、5、…,其中数字“1”在页码中共出现200次。

答案： 200　[解析]①个位上:每10个数就出现一次，共$500÷10 = 50$（次）；②十位上:每100个数就出现10次，共$(500÷100)×10 = 50$（次）；③百位上:仅在100~199出现过，共100次。因此数字“1”在页码中出现了$50 + 50 + 100 = 200$（次）。

17. (2024 陕西 JDFZ)0 是极为重要的数字,它是由古印度人在约公元 5 世纪时发明的。在所有四位数中,数字“0”共出现2700次。

答案： 2700　[解析]四位数是1000~9999，共有9000个数，个位是0的数字有$9×10×10×1 = 900$（个）；十位是0的数字有$9×10×10×1 = 900$（个）；百位是0的数字有$9×10×10×1 = 900$（个）；千位没有是0的，所以数字“0”共出现$900 + 900 + 900 = 2700$（次）。

18. (2024 陕西 GDFZ)一本书编页码时,一共用了 62 个数字“8”,且最后一页是含有“8”的页码,则这本书共有318页。

答案： 318　[解析]如果是300页，那么个位用“8”的有:8，18，28，38，48，…，298，用了30个“8”；十位用“8”的有:80，81，82，…，89，180，181，182，…，189，280，281，282，…，289，用了30个“8”；$62−30−30 = 2$（个），因此，还需要2个8，即308，318，所以这本书共有318页。

19. (2023 陕西 AZ 中学)一本书的页码是连续的自然数:1,2,3,…,当将这些页码加起来的时候,某个页码被加了两次,得到不正确的结果 2022,则这个被加了两次的页码是6

答案： 6　[解析]设这本书共有$n$页，则$n×(n + 1)÷2＜2022$，$n×(n + 1)＜4044$，由于$63×64 = 4032$，$64×65 = 4160$，$4032＜4044＜4160$，假设$n = 63$，$2022−63×64÷2 = 6＜63$满足；假设$n = 62$，$2022−62×63÷2 = 69＞62$ 不满足。所以$n = 63$，$2022−63×64÷2 = 6$，所以被加了两次的页码是6。

20. (2024 陕西 JDFZ 少年班)从 7 开始,把 7 的倍数依次写下去,一直写到 994,成为一个很大的数。71421…987994,这个数是几位数? 如果从这个数的末位数字开始,往前截去 160 个数字,剩下部分的最末一位数字是多少?

答案： 解:$994 = 7×142$，$15×7 = 105$，$7×2 = 14$。7的倍数中，一位数有1个，是7，占的位数是1位；两位数有13个，取值范围是14~98，占的位数是26位；三位数有$142−1−13 = 128$（个），取值范围是105~994，占的位数是$128×3 = 384$（位）。所以这个数总的位数是$1 + 26 + 384 = 411$（位）。$160÷3 = 53\cdots\cdots1$，$142−53 = 89$，$89×7 = 623$，所以623中的3是被截去的第160个数字，则2为剩下部分的最末一位数字。
　　答:这个数是411位数，剩下部分的最末一位数字是2。

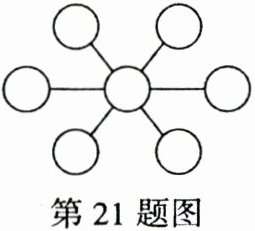
21. (2023 陕西 GXYZFD 中学)将 1~7 七个数字分别填入右图中的七个圆圈内,使每条直线上的三个圆圈内各数之和相等。
知识及方法
视频讲解

答案：
解:填数如解图。（答案不唯一）
　　　　　　　

22. (2024 重庆 KJC8Z 改编)2021 年 07 月 23 日到 08 月 08 日在日本东京举行了第 32 届奥林匹克运动会,右图是奥运会五环标志,请将 1~9 分别填入五个环相互分割的 9 个区域,使每个环内的数字和都相等,则 x 的可能值为3或4或6或8

答案： 3或4或6或8