《2025年重点中学招生分班五年真题分类卷数学》

某团体有 100 名成员,男、女成员人数之比为 14:11,成员分成三组,甲组人数与乙、丙两组人数的和一样多,若甲、乙、丙各组男、女成员的人数比是:甲组为 12:13,乙组为5:3,丙组为 2:1,则丙组中有12名男成员。

答案： 12

14. (2023 陕西 XA3Z)有大、小两筐苹果,大筐苹果与小筐苹果单价比是 5:4,其重量比是 2:3,把两筐苹果混合在一起成 100 千克的混合苹果,按单价为每千克 8.8 元出售,若总销售价格不变,大、小两筐苹果原单价各是多少?

答案： 解:设大筐苹果的单价是x元,小筐苹果的单价就是$\frac{4}{5}$x元,两筐苹果混合后,大筐苹果有100×$\frac{2}{5}$=40(千克),小筐苹果有100×$\frac{3}{5}$=60(千克),这100千克苹果一共能卖100×8.8=880(元),所以有40x +60×$\frac{4}{5}$x=880,解得x=10,$\frac{4}{5}$x=$\frac{4}{5}$×10=8(元)。答:大筐苹果的单价是10元，小筐苹果的单价是8元。

15. (2024 陕西 GDFZ)一个三角形三个内角的度数比是 7:7:14,这个三角形是(B)
A.锐角三角形
B.等腰直角三角形
C.直角三角形
D.等腰三角形

答案： B

16. (2024 陕西 GXYZFD 学校)一个长方体的棱长之和是 144 厘米,长、宽、高的比是 5:4:3,则它的体积是1620立方厘米。

答案： 1620

17. (2024 陕西 JDFZKG 学校)甲、乙、丙三人收集的邮票张数的比为 9:4:2,甲给了丙 30 张邮票,乙给了丙几张邮票后,甲、乙、丙三人的邮票张数的比变成了 2:1:1。乙给了丙几张邮票?

答案： 解:开始时甲占三人总数的$\frac{9}{9+4+2}$=$\frac{3}{5}$,结束时甲占三人总数的$\frac{2}{2+1+1}$=$\frac{1}{2}$;又知甲的邮票减少了30张,故邮票总数为30÷($\frac{3}{5}$ - $\frac{1}{2}$)=300(张)。开始时乙占三人总数的$\frac{4}{9+4+2}$=$\frac{4}{15}$,结束时乙占三人总数的$\frac{1}{2+1+1}$=$\frac{1}{4}$,则乙给了丙300×$\frac{4}{15}$−300×$\frac{1}{4}$=5(张)。答:乙给了丙5张邮票。

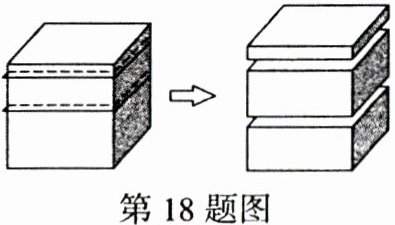
18. (2024 陕西 GDFZ)如图所示,把正方体用两个与它的底面平行的平面切开,分成三个长方体,这三个长方体的表面积之比是 3:4:5,用最简整数比表示这三个长方体的体积比。

答案： 解:设正方体的棱长为a,三个长方体的高分别为h₁,h₂、h₃,则h₁+h₂+h₃=a.由题意可得:2(ah₁+ah₁+aa):2(ah₂+ah₂+aa):2(ah₃+ah₃+aa)=3:4:5,则进行整合得出:(ah₁+ah₁+aa):(ah₂+ah₂+aa):(ah₃+ah₃+aa)=3:4:5,化简得a(2h₁+a):a(2h₂+a):a(2h₃+a)=3:4:5,即(2h₁+a):(2h₂+a):(2h₃+a)=3:4:5,假设2h₁+a=3,则2h₂+a=4,2h₃+a=5,即h₁=$\frac{3−a}{2}$,h₂=$\frac{4−a}{2}$,h₃=$\frac{5−a}{2}$,因为h₁+h₂+h₃=a,所以$\frac{3−a}{2}$+$\frac{4−a}{2}$+$\frac{5−a}{2}$=a,解得a=2.4,则h₁=0.3,h₂=0.8,h₃=1.3,高的比为0.3:0.8:1.3=3:8:13,因为底面积相等，高的比即体积的比，答:所以三个长方体体积的比是3:8:13。

19. (2021 陕西 GDFZ)某工地用三种型号的卡车运送土方,已知甲、乙、丙三种卡车载重量之比为10:7:6,速度比为 3:4:5,运送土方的路程之比为 15:14:14,三种车的辆数之比为 10:5:7。工程开始时,乙、丙两种车全部投入运输,但甲种车只有一半投入,直到 10 天后,另一半甲种车才投入工作,又干了 15 天才完成任务。求总工作量与甲种车完成的工作量之比。

答案： 解:甲、乙、丙三种车的工作时间比为20:25:25=4:5:5,三种卡车每辆的工作量之比为$\frac{10×3}{15}$:$\frac{7×4}{14}$:$\frac{6×5}{14}$=14:14:15,甲、乙、丙三种卡车完成的工作量之比为(14×10×4):(14×5×5):(15×7×5)=16:10 :15,总工作量与甲种车完成的工作量之比是(16+10+15):16=41:16。答:总工作量与甲种车完成的工作量之比是41:16。