第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
23. (2024 陕西 JDFZ)我国南宋数学家杨辉在《续古摘奇算法》中的攒九图中提出“幻圆”的概念。如图是一个最简的二阶幻圆的模型,将一些数字分别填入图中的圆圈内。要求:①外、内两个圆周上的四个数字之和相等;②外圆两直径上的四个数字之和相等,请你求图中外、内两个圆周上两空白圆圈内应填写的数字从左至右分别是
4
和7
答案:
47 [解析]内圈上的数字之和为$3 + 6 + 9 = 18$,外圈上的数字之和为$2 + 8 + 11 = 21$,相差3,而外圆直径上的数字之和分别为$2 + 3 + 9 + 11 = 25$,$6 + 8 = 14$,相差11,所以两个空白圆圈上的数字之和为11,数字之差为3,可验证得:从左至右分别为4,7。
24. (2020 成都 TFQZ)据说美国有一位铁路职工花了 50 余年的业余时间,研究得到了一个六角形幻方,如图所示的每一个圆中分别填写了 1,2,…,19 中的一个数(不同的圆中填写的数各不相同),使得图中每一个横或斜方向的线段上几个圆内的数之和都相等,现在已知该图中七个圆内的数,则图中的$x= $
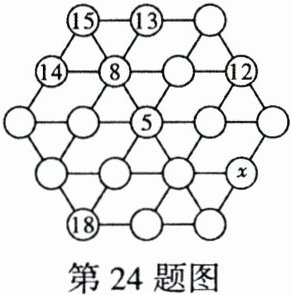

答案:
19 [解析]假设最右上角的圆中是$a$,则$15 + 13 + a=a + 12+$最右边的数,得到最右边的数是16,根据最左边的两边共有一个数及和相等,得到18左上方的数是$14 + 15−18 = 11$,然后根据各边数的和相等且为$28 + a$,将每个圆中的数都用$a$表示出来,如解图所示。因为这些数是1到19之间的数,可以得出$a$小于11,大于6。因为8已经有了,若为9,$9−4 = 5$,5已经有了;若为7,$12−7 = 5$,亦不可,故$a$只能是10,所以每一横或斜方向的数之和为38。因此$x = 38−16−3 = 19$。

19 [解析]假设最右上角的圆中是$a$,则$15 + 13 + a=a + 12+$最右边的数,得到最右边的数是16,根据最左边的两边共有一个数及和相等,得到18左上方的数是$14 + 15−18 = 11$,然后根据各边数的和相等且为$28 + a$,将每个圆中的数都用$a$表示出来,如解图所示。因为这些数是1到19之间的数,可以得出$a$小于11,大于6。因为8已经有了,若为9,$9−4 = 5$,5已经有了;若为7,$12−7 = 5$,亦不可,故$a$只能是10,所以每一横或斜方向的数之和为38。因此$x = 38−16−3 = 19$。

25. (2024 陕西 GDFZ)在图中七个小圆圈中各填入一个自然数,同时满足以下要求:
(1)使所填的七个自然数的和是 1997;
(2)使图中给的每个数都是相邻两个○中所填数的差。
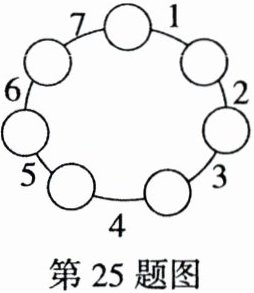
(1)使所填的七个自然数的和是 1997;
(2)使图中给的每个数都是相邻两个○中所填数的差。

答案:
解:设最上面的数为$A$,由题意得:因为1加到7的和是28,所以加号的是14,减号的是14,那么:$1−2 + 3 + 4−5 + 6−7 = 0$,即:$A + 1−2 + 3 + 4−5 + 6−7 = A$,这样七个数分别为$A$,$A + 1$,$A + 1−2 = A−1$,$A + 1−2 + 3 = A + 2$,$A + 6$,$A + 1$,$A + 7$,则:$7A + 16 = 1997$,$A = 283$,所以最上面的数是283,按顺时针的方向依次是:283,284,282,285,289,284,290,填数如解图。

解:设最上面的数为$A$,由题意得:因为1加到7的和是28,所以加号的是14,减号的是14,那么:$1−2 + 3 + 4−5 + 6−7 = 0$,即:$A + 1−2 + 3 + 4−5 + 6−7 = A$,这样七个数分别为$A$,$A + 1$,$A + 1−2 = A−1$,$A + 1−2 + 3 = A + 2$,$A + 6$,$A + 1$,$A + 7$,则:$7A + 16 = 1997$,$A = 283$,所以最上面的数是283,按顺时针的方向依次是:283,284,282,285,289,284,290,填数如解图。

26. (2022 广东 GDFDZXC)如图,圆圈内有五个数 A,B,C,D,E,方框内的数表示与它相连的所有圆圈中的平均数,则 C 是
4
答案:
4 [解析]由题图得$\begin{cases}A + B + C + D + E = 5×7 = 35\\A + B + C = 3×3 = 9\\C + D + E = 3×10 = 30\end{cases}$,所以$C=(A + B + C)+(C + D + E)-(A + B + C + D + E)=9 + 30−35 = 4$。
27. (2024 陕西 CX4Z)将 1~8 这八个自然数分别填入图中的正方体的八个顶点处的○内,并使每个面上的四个○内数字之和都相等。
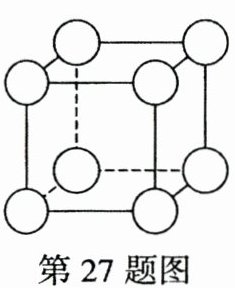

答案:
解:填数如解图。(答案不唯一)

解:填数如解图。(答案不唯一)

28. (2024 陕西 JD2FZ)如图是 3×3 的正方形,每一方格内的字母都代表某一个数,已知每行每列及对角线上三个数之和都相等,若$a= 3,d= 12,m= 15$,那么$b=$
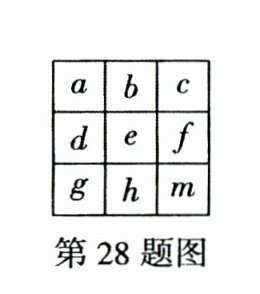
18
;$h=$0

答案:
18 0 [解析]根据题意可知,$a + d + g = a + e + m$,即$12 + g = e + 15$,$g = e + 3$;$b + e + h = g + h + m$,即 $b + e + h = e + 3 + h + 15$,$b = 18$;$a + d + g = b + e + h$,即 $15 + e + 3 = 18 + e + h$,$h = 0$。
29. (2023 陕西 TYZ)相传,大禹治水时,洛水中出现了一个“神龟”,它的背上有美妙的图案,史称“洛书”,用现在的数字翻译出来,就是三阶幻方。三阶幻方是最简单的幻方,又叫九宫格,它是由九个数字组成的一个三行三列的矩阵。其对角线、横行、纵向的数字之和均相等,这个和叫做幻和,正中间那个数叫中心数。如图,图①是由 1,2,3,4,5,6,7,8,9 所组成的一个三阶幻方,其幻和为 15,中心数为 5。图②是一个新三阶幻方,该新三阶幻方的幻和为$a_{3}$的 6 倍,且$a_{3}+a_{7}= 28$,则$a_{7}=$
21
答案:
21
查看更多完整答案,请扫码查看


