第81页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
7. 如图所示为住宅区的两栋楼,它们的高AB=CD=30m,两栋楼间的距离AC=30m,现需了解甲楼对乙楼采光的影响.
(1)当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高.(精确到0.1m)
(2)若要甲楼的影子刚好不落在乙楼墙上,此时太阳光与水平线的夹角为多少度?(√3≈1.73)
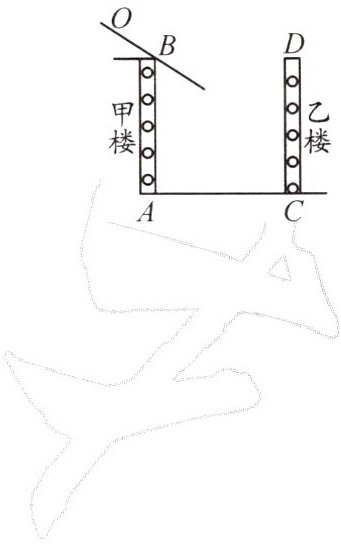
(1)当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高.(精确到0.1m)
(2)若要甲楼的影子刚好不落在乙楼墙上,此时太阳光与水平线的夹角为多少度?(√3≈1.73)

解:(1)12.7m (2)45°
答案:
解:
(1)12.7m
(2)45°
(1)12.7m
(2)45°
夜晚,小明在路灯下散步.已知小明身高1.5米,路灯的灯柱高4.5米.
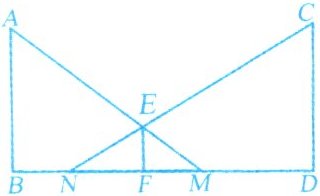
(1)如图1,若小明在相距10米的两路灯AB,CD之间行走(不含两端),他前后的两个影子长分别为FM=x,FN=y,试求y与x之间的函数关系式,并指出自变量x的取值范围.
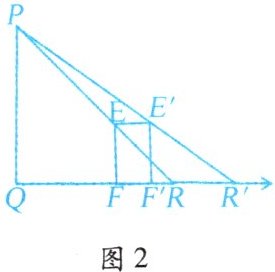
(2)“形影不离”的原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的.如图2,若小明在灯柱PQ前,朝着影子的方向(图中箭头方向)以0.8米/秒的速度匀速行走,试求他影子的顶端R在地面上移动的速度.
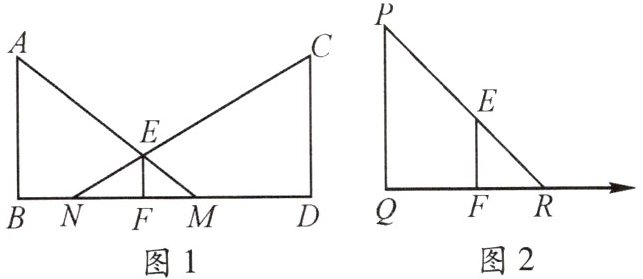
(1)如图1,若小明在相距10米的两路灯AB,CD之间行走(不含两端),他前后的两个影子长分别为FM=x,FN=y,试求y与x之间的函数关系式,并指出自变量x的取值范围.
(2)“形影不离”的原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的.如图2,若小明在灯柱PQ前,朝着影子的方向(图中箭头方向)以0.8米/秒的速度匀速行走,试求他影子的顶端R在地面上移动的速度.
解:(1)∵EF//AB,
∴∠MEF=∠A,∠MFE=∠B.
∴△MEF∽△MAB.
∵MF/MB=EF/AB=1.5/4.5=1/3.
∴x/MB=1/3,MB=3x BF=3x-x=2x.
同理,DF=2y.
∵BD=10
∴2x+2y=10
∴y=-x+5
∵当EF接近AB时,影长FM接近0;
当EF接近CD时,影长FM接近5
∴0<x<5;
(2)如图,设运动时间为t秒,则EE'=FF'=0.8t
∵EF//PQ
∴∠REF=∠RPQ,∠RFE=∠RQP
∴△REF∽△RPQ
∴RE/RP=EF/PQ=1.5/4.5=1/3,
∴PE/RP=2/3,
∵EE'//RR'
∴∠PEE'=∠PRR',∠PE'E=∠PR'R
∴△PEE'∽△PRR'
∴EE'/RR'=PE/RP,
∴0.8t/RR'=2/3,
∴RR'=1.2t,
∴V影子=1.2t/t=1.2米/秒.
∴∠MEF=∠A,∠MFE=∠B.

∴△MEF∽△MAB.
∵MF/MB=EF/AB=1.5/4.5=1/3.
∴x/MB=1/3,MB=3x BF=3x-x=2x.
同理,DF=2y.
∵BD=10
∴2x+2y=10
∴y=-x+5
∵当EF接近AB时,影长FM接近0;
当EF接近CD时,影长FM接近5
∴0<x<5;
(2)如图,设运动时间为t秒,则EE'=FF'=0.8t
∵EF//PQ
∴∠REF=∠RPQ,∠RFE=∠RQP
∴△REF∽△RPQ
∴RE/RP=EF/PQ=1.5/4.5=1/3,
∴PE/RP=2/3,
∵EE'//RR'
∴∠PEE'=∠PRR',∠PE'E=∠PR'R
∴△PEE'∽△PRR'
∴EE'/RR'=PE/RP,
∴0.8t/RR'=2/3,
∴RR'=1.2t,
∴V影子=1.2t/t=1.2米/秒.


答案:
解:
(1)
∵EF//AB,
∴∠MEF=∠A,∠MFE=∠B.

∴△MEF∽△MAB.
∵MF/MB=EF/AB=1.5/4.5=1/3.
∴x/MB=1/3,MB=3x BF=3x-x=2x.
同理,DF=2y.
∵BD=10
∴2x+2y=10
∴y=-x+5
∵当EF接近AB时,影长FM接近0;
当EF接近CD时,影长FM接近5
∴0<x<5;
(2)如图,设运动时间为t秒,则EE'=FF'=0.8t
∵EF//PQ
∴∠REF=∠RPQ,∠RFE=∠RQP
∴△REF∽△RPQ
∴RE/RP=EF/PQ=1.5/4.5=1/3,
∴PE/RP=2/3,
∵EE'//RR'
∴∠PEE'=∠PRR',∠PE'E=∠PR'R
∴△PEE'∽△PRR'
∴EE'/RR'=PE/RP,
∴0.8t/RR'=2/3,
∴RR'=1.2t,
∴V影子=1.2t/t=1.2米/秒.
解:
(1)
∵EF//AB,
∴∠MEF=∠A,∠MFE=∠B.

∴△MEF∽△MAB.
∵MF/MB=EF/AB=1.5/4.5=1/3.
∴x/MB=1/3,MB=3x BF=3x-x=2x.
同理,DF=2y.
∵BD=10
∴2x+2y=10
∴y=-x+5
∵当EF接近AB时,影长FM接近0;
当EF接近CD时,影长FM接近5
∴0<x<5;
(2)如图,设运动时间为t秒,则EE'=FF'=0.8t
∵EF//PQ
∴∠REF=∠RPQ,∠RFE=∠RQP
∴△REF∽△RPQ
∴RE/RP=EF/PQ=1.5/4.5=1/3,
∴PE/RP=2/3,
∵EE'//RR'
∴∠PEE'=∠PRR',∠PE'E=∠PR'R
∴△PEE'∽△PRR'
∴EE'/RR'=PE/RP,
∴0.8t/RR'=2/3,
∴RR'=1.2t,
∴V影子=1.2t/t=1.2米/秒.
查看更多完整答案,请扫码查看


