《2025年育才金典九年级数学全一册北师大版》

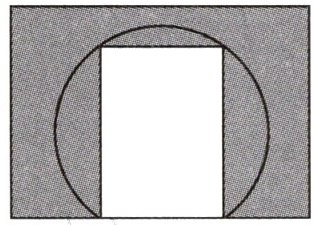
6. 一面墙上有一个矩形门洞，其中宽为1.5米，高为2米. 现要将其改造成圆弧形门洞(如图)，则改造后圆弧形门洞的最大高度是 2.25米.

答案： 2.25米

7. 一个半圆形桥洞的截面如图所示，O为圆心，直径AB是河底线，弦CD是水位线，CD//AB，且AB=26 m，OE⊥CD于点E. 水位正常时测得OE:CD=5:24. (1)求CD的长. (2)现汛期来临，水面要以每小时4 m的速度上升，则经过多长时间桥洞会刚刚被灌满? 解：(1)CD=24 m (2)t=2

答案： 解：
(1)CD=24 m
(2)t=2

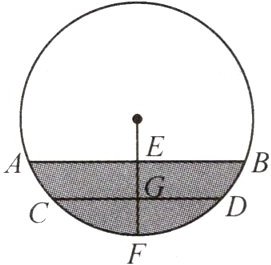
8. 如图，圆柱形水管内原有积水的水平面宽CD=20 cm，水深GF=2 cm. 若水面上升2 cm(EG=2 cm)，则此时水面宽AB= $16\sqrt{3}$ cm.

答案： $16\sqrt{3}$

9. 如图，OM,ON为相交成30°角的两条公路，在OM上距O处800米的A处有一所学校，一拖拉机以每小时36千米的速度从O处向N处行驶. 若它与学校的距离不超过500米时会对学校产生影响，问拖拉机噪音影响学校的时间为多长? 解：由图可知：以500为半径画圆，分别交ON于B,C两点，AD⊥BC，BD=CD=$\frac{1}{2}$BC，OA=800m，∵在Rt△AOD中，∠AOB=30°，∴AD=$\frac{1}{2}$OA=$\frac{1}{2}×800=400m$，在Rt△ABD中，AB=500，AD=400，由勾股定理得：BD=$\sqrt{AB^2 - AD^2}=\sqrt{500^2 - 400^2}=300m$，故BC=2×300=600米，即拖拉机在经过BC时对学校产生影响. ∵拖拉机的速度为36千米/小时，即$\frac{36000}{60}=600$米/分钟，拖拉机经过BC时需要600÷600=1分钟.

答案： 解：由图可知：以500为半径画圆，分别交ON于B,C两点，AD⊥BC，BD=CD=$\frac{1}{2}$BC，OA=800m，
∵在Rt△AOD中，∠AOB=30°，
∴AD=$\frac{1}{2}$OA=$\frac{1}{2}×800=400m$，在Rt△ABD中，AB=500，AD=400，由勾股定理得：BD=$\sqrt{AB^2 - AD^2}=\sqrt{500^2 - 400^2}=300m$，故BC=2×300=600米，即拖拉机在经过BC时对学校产生影响.
∵拖拉机的速度为36千米/小时，即$\frac{36000}{60}=600$米/分钟，拖拉机经过BC时需要600÷600=1分钟.

人工浮床又称人工浮岛，自20年前人类开发出第一个人工浮床之后，就将人工浮床应用于地表水体的污染治理和生态修复. 近年来，我国的人工浮床技术开发及应用处于快速发展时期. 如图所示是我市在某湖面上为净化水质而搭建的一个水上圆形人工浮床示意图，其中圆和三块边长为16米的正方形是浮床框架部分，被分割成的7个部分将运用无土技术分

别

栽培7种不同的水生植物，正方形的顶点A,B,C,D都在圆上，且整个浮床成轴对称图形. 求这个圆形人工浮床的半径. 解：连接BD交EF于P，过P作PO⊥BD交HG于O，连接OB，在△BEP与△PDQ中，∠E=∠DQP，∠EPB=∠EPQ，BE=EQ，∴△BEP≌△DQP，∴PB=PD，∴点O为圆心，∵BD=$\sqrt{32^2 + 24^2}=40$，∴PB=20，∴PE=$\sqrt{PB^2 - BE^2}=12$，∴PH=4，∵∠E=∠EHG=90°，∴∠EBP + ∠EPB=∠EPB + ∠HPO=90°，∴∠EPB=∠HPO，∴△PBE∽△POH，∴$\frac{PH}{BE}=\frac{HO}{PE}$，∴HO=3，∴OG=13，∴OB=$\sqrt{BG^2 + OG^2}=5\sqrt{17}$，∴这个圆形人工浮床的半径为$5\sqrt{17}$米.

答案： 解：连接BD交EF于P，过P作PO⊥BD交HG于O，连接OB，在△BEP与△PDQ中，∠E=∠DQP，∠EPB=∠EPQ，BE=EQ，
∴△BEP≌△DQP，
∴PB=PD，
∴点O为圆心，
∵BD=$\sqrt{32^2 + 24^2}=40$，
∴PB=20，
∴PE=$\sqrt{PB^2 - BE^2}=12$，
∴PH=4，
∵∠E=∠EHG=90°，
∴∠EBP + ∠EPB=∠EPB + ∠HPO=90°，
∴∠EPB=∠HPO，
∴△PBE∽△POH，
∴$\frac{PH}{BE}=\frac{HO}{PE}$，
∴HO=3，
∴OG=13，
∴OB=$\sqrt{BG^2 + OG^2}=5\sqrt{17}$，
∴这个圆形人工浮床的半径为$5\sqrt{17}$米.