《2025年育才金典九年级数学全一册北师大版》

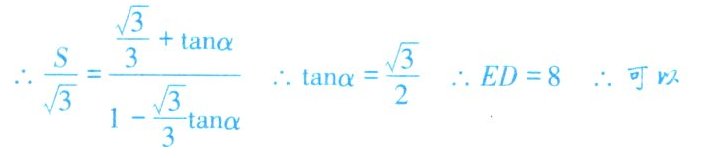
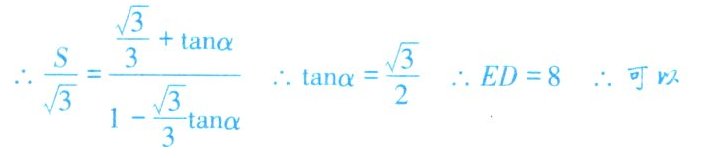
如图,在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距8√3km的C处.(1)求该轮船航行的速度.(保留精确结果)(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.解:(1)12√7(km/n) (2)延长BC交直线MN于点D,设∠BDA=α 则tan∠BCA=tan(30°+α) ∴ S/√3=(√3/3 + tanα)/(1 - √3/3 tanα) ∴tanα=√3/2 ∴ED=8 ∴可以

答案： 解:
(1)12√7(km/n)
(2)延长BC交直线MN于点D,设∠BDA=α 则tan∠BCA=tan(30°+α)
∴ S/√3=(√3/3 + tanα)/(1 - √3/3 tanα)
∴tanα=√3/2
∴ED=8
∴可以

当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做 仰角,视线在水平线下方的角叫做 俯角.

答案： 仰角; 俯角

1. 测量底部可以到达的物体的高度.(请画出图形,并找出要测的数据)
方法一:(利用镜面反射)
方法二:(利用测倾器测角)
方法三:(利用阳光下同一时刻物高与影长的比相等)

答案： 答题卡
1. 测量底部可以到达的物体的高度
图形：
（由于文本限制，描述图形如下，实际需画简图）
设物体为 $AB$，底部 $B$ 点可到达，观测点为 $C$ 点，与 $B$ 点水平距离为 $a$。
方法一（利用镜面反射）：
步骤：
1. 在 $B$ 点放置镜面，后退至 $C$ 点，使能看到 $A$ 点在镜中的像。
2. 测量 $BC$ 的距离 $a$，以及 $C$ 点到镜面（即 $B$ 点）的垂直高度（若镜面放地面，则为 $0$，或忽略）。
3. 测量眼睛（或测点）到地面的高度 $h'$，以及镜面反射中视线与地面的夹角对应的正切值（或直接测角），或通过相似三角形计算。
4. 设 $\theta$ 为视线与地面的夹角，则 $AB = BC × \tan(\theta) + h'$（若镜面放地面，$h'$ 为眼睛高度，需调整公式）。
简化公式（镜面放地面，忽略镜面厚度）：
$AB = a × \tan(\theta) + h'$，其中 $\theta$ 为视线与地面夹角，$h'$ 为眼睛高度。
方法二（利用测倾器测角）：
步骤：
1. 在 $C$ 点用测倾器测 $A$ 点的仰角 $\alpha$。
2. 测量 $BC$ 的水平距离 $a$。
3. 测量 $C$ 点到地面的高度 $h'$（若 $C$ 点与 $B$ 点等高，可忽略）。
4. 计算：$AB = a × \tan(\alpha) + h'$。
方法三（利用阳光下同一时刻物高与影长的比相等）：
步骤：
1. 测量物体 $AB$ 的影长 $b$。
2. 测量已知高度 $h'$ 的物体（如人）的影长 $b'$。
3. 由相似三角形得：$\frac{AB}{b} = \frac{h'}{b'}$。
4. 计算：$AB = \frac{h' × b}{b'}$。
最终结论：
方法一、二、三均可测量底部可以到达的物体高度，具体选择取决于实际条件和工具。

2. 测量底部不可到达物体的高度.
如图,物体AB与测量点之间有一池塘，测量物体AB的高度可按下列步骤进行：
(1)在测量点M处安置 测倾器,测得此时点B的仰角∠BNE=α；
(2)在测量点C(点A,C,M在同一直线上)处安置测倾器,测得此时点B的仰角∠BDE=β；
(3)量出侧倾器的高CD=MN=a,MC=b,由此计算出物体的高度AB= a + $\frac{b \tan\beta \cdot \tan\alpha}{\tan\beta - \tan\alpha}$.

答案： 测倾器; a + $\frac{b \tan\beta \cdot \tan\alpha}{\tan\beta - \tan\alpha}$

例1 如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°；再往塔的方向前进50 m至B处,测得仰角为60°.那么该塔有多高？（小明的身高忽略不计，结果精确到1 m,$\sqrt{3}\approx1.73$）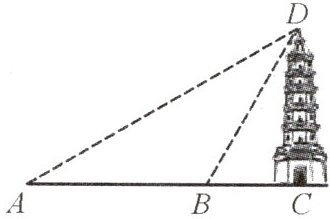
解：CD=25$\sqrt{3}\approx43$m

答案： 解：CD=25$\sqrt{3}\approx43$m