《2025年育才金典九年级数学全一册北师大版》

例2 如图，在$Rt\triangle ACB$中，$\angle C = 90°$，$AC = 6\ cm$，$CB = 8\ cm$. 点$P$，$Q$同时由$A$，$B$两点出发，分别沿$AC$，$BC$方向向点$C$匀速移动，它们的速度都是1 cm/s. 问几秒后$\triangle PCQ$的面积为$Rt\triangle ACB$面积的一半？

解：设经过$x$秒后$\triangle PCQ$的面积是$Rt\triangle ACB$面积的一半，
则：$\dfrac{(8 - x)(6 - x)}{2} = 12$，
解得$x_1 = 12$（舍去），$x_2 = 2$.
答：经2秒$\triangle PCQ$的面积是$Rt\triangle ACB$面积的一半.

答案： 解：设经过$x$秒后$\triangle PCQ$的面积是$Rt\triangle ACB$面积的一半。
$Rt\triangle ACB$的面积为$\dfrac{1}{2} × AC × CB = \dfrac{1}{2} × 6 × 8 = 24\ cm^2$，其一半为$12\ cm^2$。
由题意得，$AP = x\ cm$，$BQ = x\ cm$，则$PC = (6 - x)\ cm$，$QC = (8 - x)\ cm$。
$\triangle PCQ$的面积为$\dfrac{1}{2} × PC × QC = \dfrac{1}{2}(6 - x)(8 - x)$。
依题意列方程：$\dfrac{1}{2}(6 - x)(8 - x) = 12$
整理得：$(6 - x)(8 - x) = 24$
$48 - 6x - 8x + x^2 = 24$
$x^2 - 14x + 24 = 0$
解得：$x_1 = 2$，$x_2 = 12$
因为$x = 12$时，$PC = 6 - 12 = -6$（不合题意，舍去）
所以$x = 2$
答：经2秒$\triangle PCQ$的面积是$Rt\triangle ACB$面积的一半。

例3 如图，某海军基地位于$A$处，在其正南方向200海里处有一重要目标$B$，在$B$的正东方向200海里处有一重要目标$C$，小岛$D$位于$AC$的中点，岛上有一补给码头，小岛$F$位于$BC$上且恰好处于小岛$D$的正南方向. 一艘军舰从$A$出发，经$B$到$C$匀速巡航，一艘补给船同时从$D$出发，沿南偏西方向匀速直线航行，欲将一批物品送达军舰.
（1）小岛$D$和小岛$F$相距多少海里？
（2）已知军舰的速度是补给船的2倍，军舰在由$B$到$C$的途中与补给船相遇于点$E$处，那么相遇时补给船航行了多少海里？

解：（1）100海里
（2）$200 - \dfrac{100\sqrt{6}}{3}$海里

答案： （1）100海里
（2）设补给船航行距离为$x$海里，军舰航行距离为$2x$海里。军舰从A到B行驶200海里，从B到E行驶$2x - 200$海里，E点坐标为$(2x - 200, 0)$。D点坐标$(100, 100)$，由距离公式得$\sqrt{(2x - 300)^2 + 100^2} = x$，平方化简得$3x^2 - 1200x + 100000 = 0$，解得$x = 200 - \frac{100\sqrt{6}}{3}$（舍去$200 + \frac{100\sqrt{6}}{3}$）。
$200 - \frac{100\sqrt{6}}{3}$海里

例4 《九章算术》“勾股”章有一题：“今有二人同所立. 甲行率七，乙行率三. 乙东行，甲南行十步而斜东北与乙会. 问甲乙行各几何？”大意是：已知甲、乙二人同时从同一地点出发，甲的速度为7，乙的速度为3. 乙一直向东走，甲先向南走10步，后又斜向北偏东方向走了一段后与乙相遇. 那么相遇时，甲、乙各走了多远？

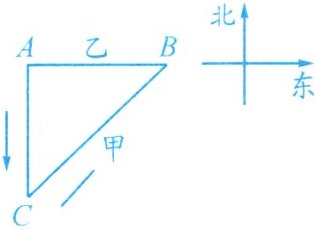
解：设经$x$秒二人在$B$处相遇，这时乙共行$AB = 3x$，
甲共行$AC + BC = 7x$，
$\because AC = 10$，
$\therefore BC = 7x - 10$，
又$\because \angle A = 90°$，
$\therefore BC^2 = AC^2 + AB^2$，
$\therefore (7x - 10)^2 = 10^2 + (3x)^2$，
$\therefore x = 0$（舍去）或$x = 3.5$，
$\therefore AB = 3x = 10.5$，
$AC + BC = 7x = 24.5$，
答：甲走了24.5步，乙走了10.5步.

答案： 设经$x$秒二人在$B$处相遇，这时乙共行$AB = 3x$，
甲共行$AC + BC = 7x$，
$\because AC = 10$（步），
$\therefore BC = 7x - 10$，
又$\because \angle A = 90°$，
在$Rt \bigtriangleup ABC$中，
$\because BC^2 = AC^2 + AB^2$，
$\therefore (7x - 10)^2 = 10^2 + (3x)^2$，
展开并整理得：
$49x^2 - 140x + 100 = 100 + 9x^2$，
$40x^2 - 140x = 0$，
$40x(x - 3.5) = 0$，
$\therefore x = 0$（舍去）或$x = 3.5$，
$\therefore AB = 3x = 3 × 3.5 = 10.5$（步），
$AC + BC = 7x = 7 × 3.5 = 24.5$（步），
答：甲走了$24.5$步，乙走了$10.5$步。

1. 某种品牌运动服经过两次降价，每件零售价由460元降为215元，已知两次降价的百分率相同，求每次降价的百分率. 设每次降价的百分率为$x$，下列方程中正确的是（B）

A.$460(1 + x)^2 = 215$
B.$460(1 - x)^2 = 215$
C.$460(1 - 2x)^2 = 215$
D.$460(1 - x^2) = 215$

答案： B

2. 一个多边形有9条对角线，则这个多边形的边有（A）

A.6条
B.7条
C.8条
D.9条

答案： A

3. 参加一次足球联赛的每两队之间都进行一场比赛，共有比赛55场，总共有11支球队参加比赛.

答案： 11

4. 一张桌子的桌面长为6米，宽为4米，台布面积是桌面面积的2倍. 如果将台布铺在桌子上，各边垂下的长度相同，求这块台布的长和宽.
解：长为8m,宽为6m.

答案： 设各边垂下的长度为$x$米。
桌面面积为$6 × 4 = 24$（平方米）。
台布面积为桌面面积的2倍，即$24 × 2 = 48$（平方米）。
台布的长为$(6 + 2x)$米，宽为$(4 + 2x)$米。
根据台布面积公式，有：
$(6 + 2x)(4 + 2x) = 48$
展开得：
$24 + 12x + 8x + 4x^2 = 48$
整理得：
$4x^2 + 20x - 24 = 0$
除以4得：
$x^2 + 5x - 6 = 0$
因式分解得：
$(x + 6)(x - 1) = 0$
解得：
$x = 1$ 或 $x = -6$（舍去负值，因为长度不能为负）。
将$x = 1$代入台布的长和宽公式中，得：
长为$6 + 2 × 1 = 8$（米），
宽为$4 + 2 × 1 = 6$（米）。
答：这块台布的长为8米，宽为6米。