第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
3. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=$\sqrt{3}$,BD=2$\sqrt{3}$.求AB及∠B.

解:AB=6 ∠B=30°

答案:
解:AB=6 ∠B=30°
4. 在一次数学活动课上,老师带领学生去测一条南北流向的河的宽度.如图,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上;沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上.请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数据:tan31°≈$\frac{3}{5}$,sin31°≈$\frac{1}{2}$)
B组

解:河宽30m.
B组
答案:
解:河宽30m.
5. 因申办2022年冬奥会,需改变哈尔滨市的交通状况.在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心、半径与AB等长的圆形危险区.现在某工人站在离B点3米远的D处,从C处测得树的顶点A的仰角为60°,树的底部B点的俯角为30°,如图所示.问距离B点8米远的保护物是否在危险区内?

解:AB=4$\sqrt{3}\lt8$ ∴无危险.
答案:
解:AB=4$\sqrt{3}\lt8$
∴无危险.
∴无危险.
视野拓展 2024年,中国国产游戏大作《黑神话:悟空》一经上线,即火爆全球,反映了中国文化的对全世界的吸引力.作为重要取景地的济南四门塔是中国现存唯一的隋代石塔,也是中国现存最早、保存最完整的单层亭阁式佛塔.某兴趣小组利用所学知识开展以“测量四门塔的高度”为主题的活动,并写出如下报告:课题 测量四门塔的高度 测量工具 测角仪、无人机等 测量示意图 测量过程 如图2,测量小组使无人机在点A处以6.8 m/s的速度竖直上升5 s后,飞行至点B处,在点B处测得塔顶D的俯角为20°;然后沿水平方向向左飞行至点C处,在点C处测得塔顶D和点A处的俯角均为45°.说明 点A,B,C,D,E均在同一竖直平面内,且点A,E在同一水平线,DE⊥AE.(结果精确到1 m;参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)(1)求无人机从点B处到点C处的飞行距离;(2)求四门塔DE的高度.
测量过程 如图2,测量小组使无人机在点A处以6.8 m/s的速度竖直上升5 s后,飞行至点B处,在点B处测得塔顶D的俯角为20°;然后沿水平方向向左飞行至点C处,在点C处测得塔顶D和点A处的俯角均为45°.说明 点A,B,C,D,E均在同一竖直平面内,且点A,E在同一水平线,DE⊥AE.(结果精确到1 m;参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)(1)求无人机从点B处到点C处的飞行距离;(2)求四门塔DE的高度.
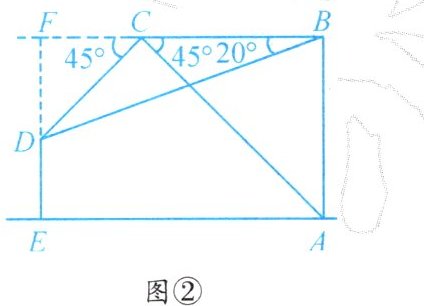
 测量过程 如图2,测量小组使无人机在点A处以6.8 m/s的速度竖直上升5 s后,飞行至点B处,在点B处测得塔顶D的俯角为20°;然后沿水平方向向左飞行至点C处,在点C处测得塔顶D和点A处的俯角均为45°.说明 点A,B,C,D,E均在同一竖直平面内,且点A,E在同一水平线,DE⊥AE.(结果精确到1 m;参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)(1)求无人机从点B处到点C处的飞行距离;(2)求四门塔DE的高度.
测量过程 如图2,测量小组使无人机在点A处以6.8 m/s的速度竖直上升5 s后,飞行至点B处,在点B处测得塔顶D的俯角为20°;然后沿水平方向向左飞行至点C处,在点C处测得塔顶D和点A处的俯角均为45°.说明 点A,B,C,D,E均在同一竖直平面内,且点A,E在同一水平线,DE⊥AE.(结果精确到1 m;参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)(1)求无人机从点B处到点C处的飞行距离;(2)求四门塔DE的高度.解:(1)由题意可知:AB=6.8×5=34(m),在Rt△ABC中,∠ABC=90°,∠ACB=45°,则BC=AB=34 m,答:无人机从点B到点C处的飞行距离为34 m;(2)如图②,延长ED交BC的延长线于点F,则四边形ABFE为矩形,∴EF=AB=34 m,设DE=x m,则DF=(34 - x)m,在Rt△DFC中,∠DFC=45°,则FC=DF=(34 - x)m,∴BF=CF + BC=(68 - x)m,在Rt△BFD中,∠FBD=20°,∵tan∠FBD=$\frac{DF}{BF}$,∴DF=BF·tan∠FBD,即34 - x=(68 - x)×0.36,解得:x≈15,答:四门塔DE的高度约为15 m.

答案:
解:(1)由题意可知:AB=6.8×5=34(m),在Rt△ABC中,∠ABC=90°,∠ACB=45°,则BC=AB=34 m,答:无人机从点B到点C处的飞行距离为34 m;(2)如图②,延长ED交BC的延长线于点F,则四边形ABFE为矩形,
∴EF=AB=34 m,设DE=x m,则DF=(34 - x)m,在Rt△DFC中,∠DFC=45°,则FC=DF=(34 - x)m,
∴BF=CF + BC=(68 - x)m,在Rt△BFD中,∠FBD=20°,
∵tan∠FBD=$\frac{DF}{BF}$,
∴DF=BF·tan∠FBD,即34 - x=(68 - x)×0.36,解得:x≈15,答:四门塔DE的高度约为15 m.
∴EF=AB=34 m,设DE=x m,则DF=(34 - x)m,在Rt△DFC中,∠DFC=45°,则FC=DF=(34 - x)m,
∴BF=CF + BC=(68 - x)m,在Rt△BFD中,∠FBD=20°,
∵tan∠FBD=$\frac{DF}{BF}$,
∴DF=BF·tan∠FBD,即34 - x=(68 - x)×0.36,解得:x≈15,答:四门塔DE的高度约为15 m.
查看更多完整答案,请扫码查看


