《2025年学典四川九年级数学全一册北师大版》

1. 如果$C是线段AB$的黄金分割点,并且$AC＞CB$,$AB = 1$,那么$AC$的长度为(C)
A.$\frac{2}{3}$
B.$\frac{1}{2}$
C.$\frac{\sqrt{5}-1}{2}$
D.$\frac{3-\sqrt{5}}{2}$

答案： C

2. 把$2$米的线段进行黄金分割,则分成的较短的线段长为(A)
A.$(3-\sqrt{5})$米
B.$(\sqrt{5}-1)$米
C.$(1+\sqrt{5})$米
D.$(3+\sqrt{5})$米

答案： A

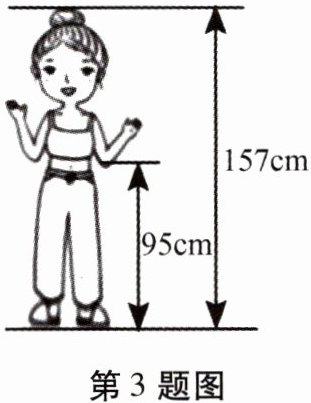
3. 当人体下半身长与身高的比值越接近$0.618$时,越给人一种美感. 如图,某女士身高$157cm$,下半身长为$95cm$,为尽可能达到美的效果,她应穿的高跟鞋的高度大约为(C)

A.$4cm$
B.$5cm$
C.$6cm$
D.$7cm$

答案： C

4. 如图,乐器上的一根弦$AB = 80cm$,两端点$A$,$B$固定在乐器面板上,其支撑点$C是AB的黄金分割点(AC＞BC)$,则$AC$的长是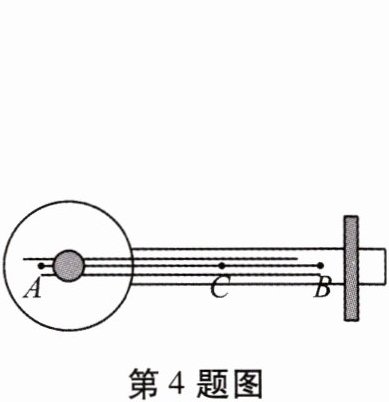$40\sqrt{5}-40$$cm$.

答案： $40\sqrt{5}-40$

5. 把一根长为$4m$的铁丝弯成一个矩形框,使它的宽与长的比为黄金比$\frac{\sqrt{5}-1}{2}$,则这个矩形的面积为$4\sqrt{5}-8$.

答案： $4\sqrt{5}-8$

6. 已知$P是线段AB$的黄金分割点,且$AP＞BP$,那么$\frac{AP - BP}{BP}$的值为$\frac{\sqrt{5}-1}{2}$.

答案： $\frac{\sqrt{5}-1}{2}$

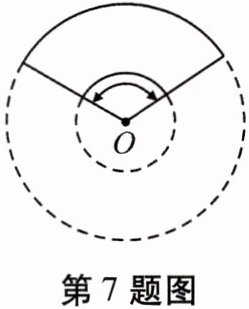
7. “黄金分割”在人类历史上有着重要的作用和影响,世界上许多著名的建筑和艺术品中都蕴涵着“黄金分割”. 下面我们就用黄金分割来设计一把富有美感的纸扇,如图,假设纸扇张开到最大时,扇形的面积与扇形所在圆的剩余部分面积的比值等于黄金比,请你来求一求纸扇张开的角度.(黄金比取$0.6$,扇形的面积公式$S= \frac{n\pi R^{2}}{360^{\circ}}$,$n$为扇形圆心角度数,$R$为扇形的半径)

答案： 设纸扇张开的角度为$n^{\circ}$，扇形半径为$R$。
扇形面积$S_1 = \frac{n\pi R^{2}}{360}$，剩余部分面积$S_2=\frac{(360 - n)\pi R^{2}}{360}$。
已知$\frac{S_1}{S_2}=0.6$，即$\frac{\frac{n\pi R^{2}}{360}}{\frac{(360 - n)\pi R^{2}}{360}} = 0.6$。
化简得$\frac{n}{360 - n}=0.6$。
$n = 0.6×(360 - n)$
$n = 216 - 0.6n$
$n + 0.6n = 216$
$1.6n = 216$
$n = 135$
所以纸扇张开的角度为$135^{\circ}$。

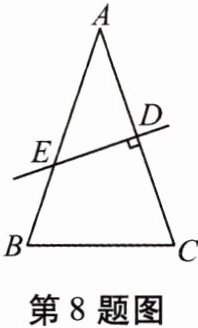
8. 如图,在$\triangle ABC$中,$AB = AC$,$AC的垂直平分线DE交AC于点D$,交$AB于点E$,若$AE = BC$,则点$E是线段AB$的黄金分割点吗？说明你的理由.

答案： 是。
设$AE = x$，$AB = AC = y$。
∵$DE$是$AC$的垂直平分线，
∴$AE = EC$（垂直平分线性质）。
∵$AE = BC$，
∴$EC = BC = x$，故$\triangle BEC$中$\angle BEC=\angle B$。
设$\angle B=\angle C=\alpha$，则$\triangle ABC$中$\angle A=180^\circ - 2\alpha$。
∵$AE = EC$，
∴$\triangle AEC$中$\angle A=\angle ACE=180^\circ - 2\alpha$。
∵$\angle ACB=\angle ACE+\angle BCE$，即$\alpha=(180^\circ - 2\alpha)+\angle BCE$，得$\angle BCE=3\alpha - 180^\circ$。
在$\triangle BEC$中，$\angle B+\angle BEC+\angle BCE=180^\circ$，即$\alpha+\alpha+(3\alpha - 180^\circ)=180^\circ$，解得$\alpha=72^\circ$，故$\angle A=36^\circ$，$\angle BCE=36^\circ$。
∵$\triangle ABC$与$\triangle EBC$中，$\angle B=\angle B$，$\angle A=\angle BCE=36^\circ$，
∴$\triangle ABC\sim\triangle EBC$（AA相似）。
∴$\frac{AB}{BC}=\frac{BC}{BE}$，即$\frac{y}{x}=\frac{x}{y - x}$，整理得$x^2=y(y - x)$。
设$\frac{x}{y}=k$，则$k^2=1 - k$，解得$k=\frac{\sqrt{5}-1}{2}$（舍负）。
∵$AE = x$，$AB = y$，$BE=y - x$，
∴$\frac{AE}{AB}=\frac{BE}{AE}=\frac{\sqrt{5}-1}{2}$。
故点$E$是线段$AB$的黄金分割点。