《2025年学典四川九年级数学全一册北师大版》

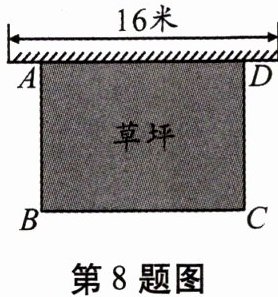
8. 如图,某幼儿园有一道长为$16$米的墙,计划用$32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD$。求该矩形草坪$BC$边的长。

答案： 设BC边的长为$x$米（BC为平行于墙的边），垂直于墙的边AB和CD的长为$y$米。
根据题意，围栏长度为32米，面积为120平方米，可得方程组：
$\begin{cases}x + 2y = 32 \\xy = 120\end{cases}$
由第一个方程得$y = \frac{32 - x}{2}$，代入第二个方程：
$x \cdot \frac{32 - x}{2} = 120$
化简得：
$x(32 - x) = 240 \implies x^2 - 32x + 240 = 0$
解方程$x^2 - 32x + 240 = 0$，判别式$\Delta = 32^2 - 4 × 1 × 240 = 64$，则：
$x = \frac{32 \pm \sqrt{64}}{2} = \frac{32 \pm 8}{2}$
解得$x_1 = 20$，$x_2 = 12$。
因为墙长16米，BC平行于墙，所以$x \leq 16$，$x = 20$舍去，故$x = 12$。
答：该矩形草坪BC边的长为12米。

9. 已知关于$x的方程x^{2}-3ax - 3a - 6 = 0$。
(1)求证：方程恒有两个不等实根；
(2)若$x_{1}$,$x_{2}$是该方程的两个实数根,且$(x_{1}-1)(x_{2}-1) = 1$,求$a$的值。

答案：
(1) 证明：
判别式 $\Delta = (-3a)^{2} - 4 × 1 × (-3a - 6) = 9a^{2} + 12a + 24$。
因为 $9a^{2} + 12a + 24 = 9(a + \frac{2}{3})^{2} + 20 ＞ 0$，
所以方程恒有两个不等实根。
(2)
根据韦达定理，有 $x_{1} + x_{2} = 3a$ 和 $x_{1}x_{2} = -3a - 6$。
由 $(x_{1} - 1)(x_{2} - 1) = 1$，
得 $x_{1}x_{2} - (x_{1} + x_{2}) + 1 = 1$。
代入 $x_{1} + x_{2} = 3a$ 和 $x_{1}x_{2} = -3a - 6$，
得 $-3a - 6 - 3a + 1 = 1$。
解得 $a = -1$。

10. (1)若$m$,$n是方程x^{2}+2x - 2027 = 0$的两个实数根,则$m^{2}+3m + n$的值为2025；
(2)已知$m$,$n$为不相等的实数,$m^{2}-3m = 2$,$n^{2}= 3n + 2$,则$\frac{m + 1}{m}+\frac{n^{2}+2n + 1}{n^{2}+n}$的值为$\frac{1}{2}$；
(3)对于实数$m$,$n$,定义一种运算“$\otimes$”如下：$m\otimes n= \begin{cases}m^{2}+m + n(m\geq n)\\n^{2}+m + n(m ＜ n)\end{cases} $,若$x\otimes(-2) = 10$,则实数$x$的值为3。

答案： 2025；$\frac{1}{2}$；3

11. 为丰富居民业余生活,某居民区组建筹委会,该筹委会动员居民自愿集资建立一个书刊阅览室。经预算,一共需要筹资$30000$元,其中一部分用于购买书桌、书架等设施,另一部分用于购买书刊。
(1)筹委会计划购买书刊的资金不少于购买书桌、书架等设施资金的$3$倍,问最多用多少资金购买书桌、书架等设施？
(2)经初步统计,有$200$户居民自愿参与集资,那么平均每户需集资$150$元。政府了解情况后,赠送了一批阅览室设施和书籍,这样只需参与户共集资$20000$元。经筹委会进一步宣传,自愿参与的户数在$200户的基础上增加了a\%$(其中$a ＞ 0$),则平均每户集资的资金在$150元的基础上减少了\frac{10}{9}a\%$,求$a$的值。

答案：
(1)设用于购买书桌、书架等设施的资金为$x$元，则购买书刊的资金为$(30000 - x)$元。
由题意得：$30000 - x \geq 3x$，
解得$x \leq 7500$。
答：最多用$7500$元购买书桌、书架等设施。
(2)参与户数为$200(1 + a\%)$户，平均每户集资为$150\left[1 - \frac{10}{9}a\%\right]$元。
由题意得：$200(1 + a\%) × 150\left[1 - \frac{10}{9}a\%\right] = 20000$，
化简得：$30000(1 + a\%)(1 - \frac{10}{9}a\%) = 20000$，
令$t = a\%$，则$3(1 + t)\left(1 - \frac{10}{9}t\right) = 2$，
展开得：$3\left(1 - \frac{1}{9}t - \frac{10}{9}t^2\right) = 2$，
整理得：$10t^2 + t - 3 = 0$，
解得$t_1 = 0.5$，$t_2 = -0.6$（舍去），
即$a\% = 0.5$，$a = 50$。
答：$a$的值为$50$。