《2025年教材完全解读七年级数学上册苏科版》

例5 2024·无锡质检
规定$\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad-bc$,试化简$\begin{vmatrix}-5&3x^{2}+5\\2&x^{2}-3\end{vmatrix} +(11x^{2}-5)$。
答 因为$\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad-bc$,
所以$\begin{vmatrix}-5&3x^{2}+5\\2&x^{2}-3\end{vmatrix} +(11x^{2}-5)$
$=-5(x^{2}-3)-2(3x^{2}+5)+(11x^{2}-5)$
$=-5x^{2}+15-6x^{2}-10+11x^{2}-5$
$=0$。
解题通法
与新定义有关的探究题的解题策略
(1)正确理解新定义运算,掌握对应的计算方法；
(2)将所求算式转化为普通运算；
(3)利用相应的运算法则计算求值,进而解决问题。

答案： 解：因为$\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad-bc$，
所以$\begin{vmatrix}-5&3x^{2}+5\\2&x^{2}-3\end{vmatrix} +(11x^{2}-5)$
$=-5(x^{2}-3)-2(3x^{2}+5)+(11x^{2}-5)$
$=-5x^{2}+15-6x^{2}-10+11x^{2}-5$
$=0$。

1.(2022·攀枝花中考·知识点1)下列各式不是单项式的为( )。

A.3
B.$a$
C.$\frac{b}{a}$
D.$\frac{1}{2}x^{2}y$

答案： C　[解析]$\frac{6}{a}$中分母含未知数,不是单项式。故选C。

2.(2023·宜宾中考·知识点4,5)下列计算正确的是( )。

A.$4a-2a= 2$
B.$2ab+3ba= 5ab$
C.$a+a^{2}= a^{3}$
D.$5x^{2}y-3xy^{2}= 2xy$

答案： B　[解析]A项,4a−2a=(4−2)a = 2a,则A不符合题意;
B项,2ab + 3ba=(2 + 3)ab = 5ab,则B符合题意;C项,a与a²不是同类项，无法合并，则C不符合题意;D项,5x²y与3xy²不是同类项，无法合并，则D不符合题意。

3.(2023·江西南昌期中·知识点8)一个多项式与$x^{2}-2x+1的和是3x-2$,则这个多项式为( )。

A.$-x^{2}+5x-3$
B.$-x^{2}+x-1$
C.$x^{2}-5x+3$
D.$x^{2}-5x-3$

答案： A　[解析]3x−2−(x²−2x + 1)=3x−2−x² + 2x−1 = −x² + 5x−3 故选A。

4.(2024·湖南湘西州期末·知识点8)若$A与B$都是二次多项式,则关于$A-B$的结论,下列选项中正确的是( )。

A.一定是二次式
B.可能是四次式
C.可能是一次式
D.不可能是零

答案： C　[解析]因为多项式相减,就是去括号、合并同类项,而合并同类项时只是把系数相加，字母和字母的指数不变，所以A−B的结果的次数一定不高于2,当A与B的二次项相同,一次项不相同时,A−B的结果为一次式;当A与B是两个相同的二次式时,A−B的结果为0。故选C。

5.(知识点7,8)化简。
(1)$2(2a-b)-(2b-3a)$；
(2)$5xy+y^{2}-2(4xy-y^{2}+1)$；
(3)$\frac{1}{2}(a^{2}-b)+\frac{1}{3}(a-b^{2})+\frac{1}{6}(a^{2}+b^{2})$。

答案： 解:
(1)2(2a−b)−(2b−3a)=4a−2b−2b + 3a = 7a−4b。
(2)5xy + y²−2(4xy−y² + 1)
　=5xy + y²−8xy + 2y²−2
　=−3xy + 3y²−2。
(3)$\frac{1}{2}$(a²−b)+$\frac{1}{3}$(a−b²)+$\frac{1}{6}$(a² + b²)
　=$\frac{1}{2}$a²−$\frac{1}{2}$b + $\frac{1}{3}$a−$\frac{1}{3}$b² + $\frac{1}{6}$a² + $\frac{1}{6}$b²
　=$\frac{2}{3}$a²−$\frac{1}{6}$b²−$\frac{1}{2}$b + $\frac{1}{3}$a。

6.(知识点7,8·能力点4)要使多项式$3x^{2}-2(5+x-2x^{2})+mx^{2}化简后不含x$的二次项,则$m$等于( )。

A.0
B.1
C.-1
D.-7

答案： D　[解析]3x²−2(5 + x−2x²)+mx² = 3x²−10−2x + 4x² + mx²=(7 + m)x²−2x−10,
∵3x²−2(5 + x−2x²)+mx²化简后不含x的二次项,
∴7 + m = 0,解得m = −7。

7.(知识点5,7,8·能力点5)把两张形状、大小完全相同的小长方形卡片(如图3-3-2①)不重复地放在一个底面为长方形(长为8cm,宽为6cm)的盒子底部(如图3-3-2②),盒子底面未被卡片覆盖的部分用阴影表示,则图3-3-2②中两块阴影部分周长的和是( )。


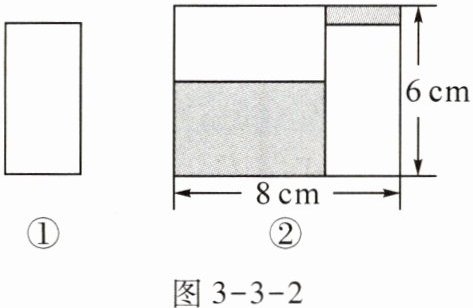
A.28 cm
B.16 cm
C.32 cm
D.24 cm

答案： D　[解析]设图①小长方形卡片的长为m cm,宽为n cm,根据题意,得两块阴影部分的周长和为2[m+(6−n)]+2[n+(6−m)]=2(m + 6−n + n−m + 6)=2×12 = 24(cm)。