第142页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
压轴1 立体图形的展开与折叠
例1 难度★★★
有一个正方体如图5-5放置(有三个面上分别标有数字4,6,8),它的平面展开图可能是下列四个选项中的( )。

图5-5
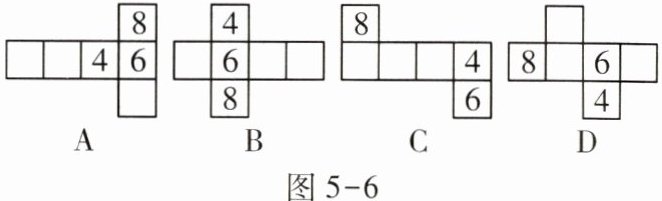
图5-6
答 A
例1 难度★★★
有一个正方体如图5-5放置(有三个面上分别标有数字4,6,8),它的平面展开图可能是下列四个选项中的( )。

图5-5

图5-6
答 A
答案:
【解析】:
本题考查正方体的展开图。
正方体的展开图有“1-4-1”型、“2-3-1”型、“2-2-2”型、“3-3”型。
需要根据正方体的特性,判断哪个选项可以折叠成带有数字4、6、8的正方体,并且数字的位置与图5-5中的正方体一致。
分析图5-5中的正方体:
正方体有三个面分别标有数字4、6、8。
数字4和6是相邻的面。
数字6和8也是相邻的面。
数字4和8是相对的面(在正方体中不相邻)。
分析选项:
A选项:
数字4和6相邻,符合。
数字6和8相邻,符合。
数字4和8相对,符合。
B选项:
数字4和6相邻,符合。
数字6和8相对,不符合(因为6和8在正方体中应该是相邻的)。
C选项:
数字4和6相对,不符合(因为4和6在正方体中应该是相邻的)。
D选项:
数字4和6相邻,符合。
数字6和8相对,不符合(因为6和8在正方体中应该是相邻的)。
因此,只有选项A满足所有条件,即数字4和6相邻,数字6和8相邻,且数字4和8相对。
【答案】:
A
本题考查正方体的展开图。
正方体的展开图有“1-4-1”型、“2-3-1”型、“2-2-2”型、“3-3”型。
需要根据正方体的特性,判断哪个选项可以折叠成带有数字4、6、8的正方体,并且数字的位置与图5-5中的正方体一致。
分析图5-5中的正方体:
正方体有三个面分别标有数字4、6、8。
数字4和6是相邻的面。
数字6和8也是相邻的面。
数字4和8是相对的面(在正方体中不相邻)。
分析选项:
A选项:
数字4和6相邻,符合。
数字6和8相邻,符合。
数字4和8相对,符合。
B选项:
数字4和6相邻,符合。
数字6和8相对,不符合(因为6和8在正方体中应该是相邻的)。
C选项:
数字4和6相对,不符合(因为4和6在正方体中应该是相邻的)。
D选项:
数字4和6相邻,符合。
数字6和8相对,不符合(因为6和8在正方体中应该是相邻的)。
因此,只有选项A满足所有条件,即数字4和6相邻,数字6和8相邻,且数字4和8相对。
【答案】:
A
用“隔一相对”法确定正方体中相对的面:正方体的展开图中相对的两个面不相连,即“上下隔一行,左右隔一列”,即“隔一相对”,而且两个面之间没有公共边或公共点。
答案:
【解析】:
题目考查的是正方体展开图中相对面的确定方法,即“隔一相对”法。这是一个空间与图形的问题,需要通过理解和应用正方体展开图的性质来解决。
“隔一相对”法指的是在正方体展开图中,相对的两个面不相连,它们之间隔了一行或一列,且没有公共边或公共点。这是确定正方体展开图中相对面的一个重要方法。
【答案】:
在正方体的展开图中,要确定相对的面,可以使用“隔一相对”法。即找到那些之间隔了一行或一列,且没有公共边或公共点的两个面,它们就是相对的面。例如,在常见的正方体展开图中,如果上面和下面、前面和后面、左面和右面是相对的,那么它们在展开图中就不会相连,而是满足“隔一相对”的条件。
题目考查的是正方体展开图中相对面的确定方法,即“隔一相对”法。这是一个空间与图形的问题,需要通过理解和应用正方体展开图的性质来解决。
“隔一相对”法指的是在正方体展开图中,相对的两个面不相连,它们之间隔了一行或一列,且没有公共边或公共点。这是确定正方体展开图中相对面的一个重要方法。
【答案】:
在正方体的展开图中,要确定相对的面,可以使用“隔一相对”法。即找到那些之间隔了一行或一列,且没有公共边或公共点的两个面,它们就是相对的面。例如,在常见的正方体展开图中,如果上面和下面、前面和后面、左面和右面是相对的,那么它们在展开图中就不会相连,而是满足“隔一相对”的条件。
例2 难度★★★★
如图5-7,将长方形ABCD绕轴l旋转一周,则形成的立体图形的体积等于( )。
$A.πr^2h$
$B.2πr^2h$
$C.3πr^2h$
$D.4πr^2h$
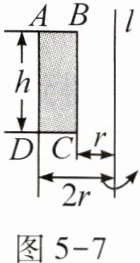
图5-7
解 体积为$π·(2r)^2·h-πr^2h= 3πr^2h。$
答 C
如图5-7,将长方形ABCD绕轴l旋转一周,则形成的立体图形的体积等于( )。
$A.πr^2h$
$B.2πr^2h$
$C.3πr^2h$
$D.4πr^2h$

图5-7
解 体积为$π·(2r)^2·h-πr^2h= 3πr^2h。$
答 C
答案:
【解析】:
本题主要考查了长方形旋转后形成的立体图形的体积计算,需要将不规则立体图形转化为规则立体图形来计算体积。
观察图形可知,将长方形$ABCD$绕轴$l$旋转一周后,形成的立体图形可以看作是一个底面半径为$2r$,高为$h$的圆柱,减去一个底面半径为$r$,高为$h$的圆柱。
根据圆柱的体积公式$V = \pi r^2h$(其中$V$为体积,$r$为底面半径,$h$为高),分别计算两个圆柱的体积:
底面半径为$2r$,高为$h$的圆柱体积$V_1 = \pi(2r)^2h = 4\pi r^2h$。
底面半径为$r$,高为$h$的圆柱体积$V_2 = \pi r^2h$。
那么所求立体图形的体积$V = V_1 - V_2 = 4\pi r^2h - \pi r^2h = 3\pi r^2h$。
【答案】:
C
本题主要考查了长方形旋转后形成的立体图形的体积计算,需要将不规则立体图形转化为规则立体图形来计算体积。
观察图形可知,将长方形$ABCD$绕轴$l$旋转一周后,形成的立体图形可以看作是一个底面半径为$2r$,高为$h$的圆柱,减去一个底面半径为$r$,高为$h$的圆柱。
根据圆柱的体积公式$V = \pi r^2h$(其中$V$为体积,$r$为底面半径,$h$为高),分别计算两个圆柱的体积:
底面半径为$2r$,高为$h$的圆柱体积$V_1 = \pi(2r)^2h = 4\pi r^2h$。
底面半径为$r$,高为$h$的圆柱体积$V_2 = \pi r^2h$。
那么所求立体图形的体积$V = V_1 - V_2 = 4\pi r^2h - \pi r^2h = 3\pi r^2h$。
【答案】:
C
图5-8
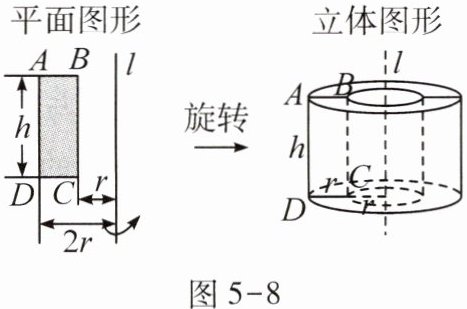
解题策略
求旋转得到的立体图形的表面积或体积主要分三步:(1)确定旋转得到的立体图形的形状;(2)将已知数据转化为立体图形中的数据;(3)根据面积或体积公式进行计算。

解题策略
求旋转得到的立体图形的表面积或体积主要分三步:(1)确定旋转得到的立体图形的形状;(2)将已知数据转化为立体图形中的数据;(3)根据面积或体积公式进行计算。
答案:
答案略
例3 难度★★★★★
用白萝卜等材料做一个正方体,并把正方体表面涂上颜色。
(1)把正方体的棱二等分,然后沿等分线把正方体切开,得到8个小正方体,观察其中三面被涂色的有a个,如图5-9①所示,那么a= ;
(2)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体,观察其中三面被涂色的有a个,各面都没有涂色的有b个,如图5-9②所示,那么a+b= ;
(3)把正方体的棱四等分,然后沿等分线把正方体切开,得到64个小正方体,观察其中两面被涂色的有c个,各面都没有涂色的有b个,如图5-9③所示,那么b+c= 。
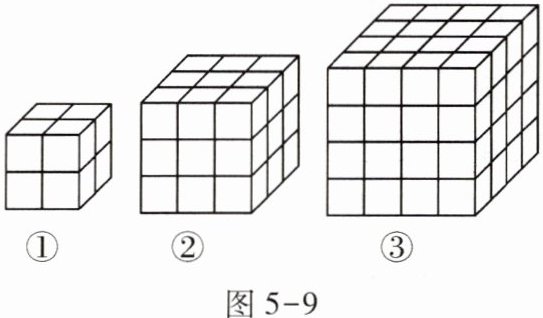
图5-9
解 (1)三面被涂色的有8个,故a= 8。
(2)三面被涂色的有8个,各面都没有涂色的有1个,故a+b= 8+1= 9。
(3)两面被涂色的有24个,各面都没有涂色的有8个,故b+c= 8+24= 32。
答 (1)8 (2)9 (3)32
必备知识 空间图形感知能力。
关键能力 充分发挥空间想象能力。
难点突破 依据“正方体顶点处的小正方体三面涂色,除顶点外位于棱上的小正方体两面涂色,位于表面中心的小正方体一面涂色,位于正中心的小正方体没有涂色”求解即可。
用白萝卜等材料做一个正方体,并把正方体表面涂上颜色。
(1)把正方体的棱二等分,然后沿等分线把正方体切开,得到8个小正方体,观察其中三面被涂色的有a个,如图5-9①所示,那么a= ;
(2)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体,观察其中三面被涂色的有a个,各面都没有涂色的有b个,如图5-9②所示,那么a+b= ;
(3)把正方体的棱四等分,然后沿等分线把正方体切开,得到64个小正方体,观察其中两面被涂色的有c个,各面都没有涂色的有b个,如图5-9③所示,那么b+c= 。

图5-9
解 (1)三面被涂色的有8个,故a= 8。
(2)三面被涂色的有8个,各面都没有涂色的有1个,故a+b= 8+1= 9。
(3)两面被涂色的有24个,各面都没有涂色的有8个,故b+c= 8+24= 32。
答 (1)8 (2)9 (3)32
必备知识 空间图形感知能力。
关键能力 充分发挥空间想象能力。
难点突破 依据“正方体顶点处的小正方体三面涂色,除顶点外位于棱上的小正方体两面涂色,位于表面中心的小正方体一面涂色,位于正中心的小正方体没有涂色”求解即可。
答案:
(1)解:三面被涂色的小正方体在正方体的顶点处,正方体有8个顶点,所以a=8。
(2)解:三面被涂色的小正方体在顶点处,有8个,即a=8;各面都没有涂色的小正方体在正方体内部,把棱三等分时,内部没有涂色的小正方体组成棱长为1的正方体,个数为1,即b=1,所以a+b=8+1=9。
(3)解:两面被涂色的小正方体在棱上(除去顶点),正方体有12条棱,棱四等分时,每条棱上两面涂色的小正方体有4-2=2个,所以c=12×2=24;各面都没有涂色的小正方体在内部,组成棱长为4-2=2的正方体,个数为2×2×2=8,即b=8,所以b+c=8+24=32。
(1)8
(2)9
(3)32
(1)解:三面被涂色的小正方体在正方体的顶点处,正方体有8个顶点,所以a=8。
(2)解:三面被涂色的小正方体在顶点处,有8个,即a=8;各面都没有涂色的小正方体在正方体内部,把棱三等分时,内部没有涂色的小正方体组成棱长为1的正方体,个数为1,即b=1,所以a+b=8+1=9。
(3)解:两面被涂色的小正方体在棱上(除去顶点),正方体有12条棱,棱四等分时,每条棱上两面涂色的小正方体有4-2=2个,所以c=12×2=24;各面都没有涂色的小正方体在内部,组成棱长为4-2=2的正方体,个数为2×2×2=8,即b=8,所以b+c=8+24=32。
(1)8
(2)9
(3)32
查看更多完整答案,请扫码查看


