第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
例2-1
设甲数为x,乙数为y,用代数式表示:
(1)甲、乙两数和的平方;
(2)甲数的2倍与乙数的$\frac{1}{3}$的和;
(3)甲、乙两数平方的差;
(4)甲、乙两数平方的和。
解 按照语言叙述的顺序,用运算符号将数或字母连接起来,从而将文字语言翻译成数学符号语言。
答 (1)$(x+y)^{2}$;(2)$2x+\frac{1}{3}y$;(3)$x^{2}-y^{2}$;(4)$x^{2}+y^{2}$。
设甲数为x,乙数为y,用代数式表示:
(1)甲、乙两数和的平方;
(2)甲数的2倍与乙数的$\frac{1}{3}$的和;
(3)甲、乙两数平方的差;
(4)甲、乙两数平方的和。
解 按照语言叙述的顺序,用运算符号将数或字母连接起来,从而将文字语言翻译成数学符号语言。
答 (1)$(x+y)^{2}$;(2)$2x+\frac{1}{3}y$;(3)$x^{2}-y^{2}$;(4)$x^{2}+y^{2}$。
答案:
【解析】:
这道题目考察的是代数式的概念,特别是如何将文字语言转化为数学符号语言。
对于每一个小问题,我们需要根据题目描述,使用适当的数学符号和运算来构建代数式。
(1) 甲、乙两数和的平方:根据描述,我们需要先求和($x+y$),然后对结果进行平方($^2$),所以代数式为 $(x+y)^{2}$。
(2) 甲数的2倍与乙数的 $\frac{1}{3}$ 的和:这里我们需要取甲数的2倍($2x$),乙数的 $\frac{1}{3}$($\frac{1}{3}y$),然后求和,所以代数式为 $2x+\frac{1}{3}y$。
(3) 甲、乙两数平方的差:我们需要分别求甲数和乙数的平方($x^{2}$ 和 $y^{2}$),然后求差,所以代数式为 $x^{2}-y^{2}$。
(4) 甲、乙两数平方的和:同样,我们先求甲数和乙数的平方,然后求和,所以代数式为 $x^{2}+y^{2}$。
【答案】:
(1) $(x+y)^{2}$
(2) $2x+\frac{1}{3}y$
(3) $x^{2}-y^{2}$
(4) $x^{2}+y^{2}$
这道题目考察的是代数式的概念,特别是如何将文字语言转化为数学符号语言。
对于每一个小问题,我们需要根据题目描述,使用适当的数学符号和运算来构建代数式。
(1) 甲、乙两数和的平方:根据描述,我们需要先求和($x+y$),然后对结果进行平方($^2$),所以代数式为 $(x+y)^{2}$。
(2) 甲数的2倍与乙数的 $\frac{1}{3}$ 的和:这里我们需要取甲数的2倍($2x$),乙数的 $\frac{1}{3}$($\frac{1}{3}y$),然后求和,所以代数式为 $2x+\frac{1}{3}y$。
(3) 甲、乙两数平方的差:我们需要分别求甲数和乙数的平方($x^{2}$ 和 $y^{2}$),然后求差,所以代数式为 $x^{2}-y^{2}$。
(4) 甲、乙两数平方的和:同样,我们先求甲数和乙数的平方,然后求和,所以代数式为 $x^{2}+y^{2}$。
【答案】:
(1) $(x+y)^{2}$
(2) $2x+\frac{1}{3}y$
(3) $x^{2}-y^{2}$
(4) $x^{2}+y^{2}$
例2-2
火车站和汽车站都为旅客提供打包服务,如果长、宽、高分别为x,y,z的箱子按如图3-2-1所示的方式打包,那么打包带的长度至少为多少?
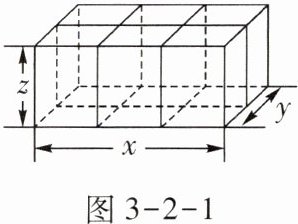
解 分别求得箱子长、宽、高方向上需要的打包带的长度,然后求和即可。
答 箱子长、宽、高方向上需要的打包带总长为$2x+4y+6z$,即打包带的长度至少为$2x+4y+6z$。
火车站和汽车站都为旅客提供打包服务,如果长、宽、高分别为x,y,z的箱子按如图3-2-1所示的方式打包,那么打包带的长度至少为多少?

解 分别求得箱子长、宽、高方向上需要的打包带的长度,然后求和即可。
答 箱子长、宽、高方向上需要的打包带总长为$2x+4y+6z$,即打包带的长度至少为$2x+4y+6z$。
答案:
解:观察图形可知,打包带在长方向上有2段,每段长度为x,共2x;在宽方向上有4段,每段长度为y,共4y;在高方向上有6段,每段长度为z,共6z。
将各方向长度相加:2x + 4y + 6z。
答:打包带的长度至少为2x + 4y + 6z。
将各方向长度相加:2x + 4y + 6z。
答:打包带的长度至少为2x + 4y + 6z。
例3
对于单项式“60x”,我们可以这样来解释:某车以60 km/h的速度行驶了x h,它一共行驶的路程是60x km。请你对“60x”再给出另一个实际生活方面的解释。
解 描述一个代数式的意义,或者从字母本身出发,来描述字母之间的数量关系,或者联系实际生活或几何背景,赋予其中的字母一定的现实意义,加以描述。
答 答案不唯一,如每本练习本的价格是x元,张翔买60本练习本要付60x元。
对于单项式“60x”,我们可以这样来解释:某车以60 km/h的速度行驶了x h,它一共行驶的路程是60x km。请你对“60x”再给出另一个实际生活方面的解释。
解 描述一个代数式的意义,或者从字母本身出发,来描述字母之间的数量关系,或者联系实际生活或几何背景,赋予其中的字母一定的现实意义,加以描述。
答 答案不唯一,如每本练习本的价格是x元,张翔买60本练习本要付60x元。
答案:
解:答案不唯一,如每支笔的价格是x元,购买60支笔需要支付60x元。
查看更多完整答案,请扫码查看


