《2025年教材完全解读七年级数学上册苏科版》

1.(知识点1)下列各式计算正确的是( )。

A.$3÷2×\frac {1}{2}= 3÷(2×\frac {1}{2})$
B.$(-1)^{4}+(-1)^{5}= 1-1$
C.$-5-2×3= (-5-2)×3$
D.$-5×2^{2}= (-5×2)^{2}$

答案： B 【解析】$3÷2×\frac {1}{2}=3×\frac {1}{2}×\frac {1}{2}≠3÷(2×\frac {1}{2})$，A 错误；$-5-2×3=-5-6≠(-5-2)×3$，C 错误；$-5×2^{2}=-5×4=-20≠(-5×2)^{2}$，D 错误。

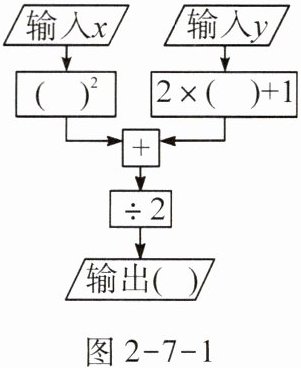
2.(知识点1)如图2-7-1,若输入的x与y满足$|x+1|+(y-\frac {1}{2})^{2}= 0$,则输出的结果为( )。


A.1.5
B.-2.5
C.-1.5
D.2.5

答案： A 【解析】因为$|x+1|+(y-\frac {1}{2})^{2}=0$，所以$x+1=0,y-\frac {1}{2}=0,$解得$x=-1,y=\frac {1}{2}$。当输入$x=-1,y=\frac {1}{2}$时，输出的结果为$[(-1)^{2}+2×\frac {1}{2}+1]÷2=(1+1+1)÷2=1.5$。

3.(知识点1·能力点1)将2,-3,-4,5进行有理数的加、减、乘、除、乘方运算,(可以用括号,但每个数字只能用一次),使得运算的结果为24,请写出一个符合要求的混合运算的式子:______= 24。

答案： $5^{2}+[(-4)-(-3)]$或$2×[4-(-3)-(-5)]$（答案不唯一）【解析】如首先用5的2次方，构造出25；然后加上-4-(-3)，使运算结果为24即可；或根据$2×12=3×8=4×6=24$来构造即可。

4.(知识点1,2·能力点1)计算下列各题。
(1)$-\frac {3^{2}}{2}×4-(-\frac {1}{4})×(-16);$
(2)$-3^{2}×(-2)^{2}+4^{2}÷(-2)^{3}-|-2^{2}|÷(-2)^{2};$
(3)$-4^{2}×[(1-7)÷6]^{3}+[(-5)^{3}-3]÷(-2)^{3};$
(4)$2^{2}÷(-0.875)×\frac {5}{4}×(-2\frac {2}{3})÷(-1\frac {3}{7})$。

答案： 解：
(1)$-\frac {3^{2}}{2}×4-(-\frac {1}{4})×(-16)$$=-\frac {9}{2}×4-(-\frac {1}{4})×(-16)$$=-18-4$$=-22$。
(2)$-3^{2}×(-2)^{2}+4^{2}÷(-2)^{3}-|-2^{2}|÷(-2)^{2}$$=-9×4+16÷(-8)-4÷4$$=-36-2-1$$=-39$。
(3)$-4^{2}×[(1-7)÷6]^{3}+[(-5)^{3}-3]÷(-2)^{3}$$=-16×(-1)+(-125-3)÷(-8)$$=16+16$$=32$。
(4)$2^{2}÷(-0.875)×\frac {5}{4}×(-2\frac {2}{3})÷(-1\frac {3}{7})$$=4÷(-\frac {7}{8})×\frac {5}{4}×(-\frac {8}{3})÷(-\frac {10}{7})$$=-4×\frac {8}{7}×\frac {5}{4}×\frac {8}{3}×\frac {7}{10}$$=-(\frac {8}{7}×\frac {7}{10})×(\frac {5}{4}×\frac {8}{3})×4$$=-\frac {32}{3}$。

5.(知识点1·能力点1)选择一个运算符号填入算式$1+[\frac {2}{3}×6□(-2)^{3}]÷(-5)$中的□位置上,若要使计算结果最小,应填入的运算符号为( )。

A.+
B.-
C.×
D.÷

答案： B 【解析】填入“+”时，原式$=1+[\frac {2}{3}×6+(-2)^{3}]÷(-5)=\frac {9}{5}$；填入“-”时，原式$=1+[\frac {2}{3}×6-(-2)^{3}]÷(-5)=-\frac {7}{5}$；填入“×”时，原式$=1+[\frac {2}{3}×6×(-2)^{3}]÷(-5)=\frac {37}{5}$；填入“÷”时，原式$=1+[\frac {2}{3}×6÷(-2)^{3}]÷(-5)=\frac {11}{10}$。$-\frac {7}{5}$最小，故选 B。

6.(知识点1·能力点1)观察下列等式:
第一个等式:$2^{2}-2^{1}= 4-2= 2= 2^{1};$
第二个等式:$2^{3}-2^{2}= 8-4= 4= 2^{2};$
第三个等式:$2^{4}-2^{3}= 16-8= 8= 2^{3};$
……
利用上述规律计算:$2^{1}+2^{2}+2^{3}+... +2^{2021}+2^{2022}-2^{2023}= $______。

答案： -2 【解析】由题意可知第n个等式为$2^{n+1}-2^{n}=2^{n};2^{1}+2^{2}+2^{3}+... +2^{2021}+2^{2022}=2^{2023}-2^{2}=2^{2}-2^{1}+2^{3}-2^{2}+2^{4}-2^{3}+... +2^{2023}-2^{2022}-2^{2023}=-2$。

7.(知识点1·能力点2)为了鼓励居民节约用水,某自来水公司采取分段计费,每月每户用水不超过$10m^{3}$,每立方米2.2元;超过$10m^{3}$的部分,每立方米加收1.3元。小明家4月份用水$15m^{3}$,应交水费______元。

答案： 39.5 【解析】$2.2×10+(2.2+1.3)×(15-10)=22+3.5×5=39.5$(元)。