《2025年教材完全解读七年级数学上册苏科版》

例1 2023·苏州中考
有理数2/3的相反数是( )。

A.-2/3
B.3/2
C.-3/2
D.±2/3

解 2/3的相反数是-2/3。
答 A

答案： 【解析】：
本题考查的是有理数的相反数的概念，根据相反数的定义，一个数与它的相反数相加结果为0，所以要求$\frac{2}{3}$的相反数，只需要改变它的符号即可。
【答案】：
解：根据相反数的定义，$\frac{2}{3}$的相反数是$-\frac{2}{3}$。
答：A

例2 2023·淄博中考
-|-3|的运算结果等于( )。

A.3
B.-3
C.1/3
D.-1/3
解 -|-3|= -3。
答 B

答案： 解：-|-3|=-3
答：B

1.(2023·栖霞期末·知识点2)下列互为相反数的是( )。

A.-(-2)与2
B.1/3与-0.33
C.-|-5|与5
D.-(+3)与+(-3)

答案： C 【解析】$-(-2)=2$，与 2 不是相反数，故 A 错误；$\frac{1}{3}$与$-0.33$不是相反数，故 B 错误；$-|-5|=-5$，与 5 是相反数，故 C 正确；$-(+3)=-3$，$+(-3)=-3$，$-3$与$-3$不是相反数，故 D 错误。

2.(2023·姑苏区期末·知识点1)下列各式中,不成立的是( )。

A.|-3|= 3
B.-|3|= -3
C.|-3|= -3
D.-|-3|= -3

答案： C 【解析】根据绝对值的定义，得$|-3|=3$。故 C 不成立。

3.(2023·建湖县期末·知识点1,2·能力点3)有理数a,b,c,d在数轴上对应点的位置如图2-3-4所示,若有理数b,d互为相反数,则这四个有理数中,绝对值最大的是 。

答案： $a$ 【解析】根据数轴上点的位置及$b$，$d$互为相反数，得$a\lt b\lt0\lt c\lt d$，且$|c|\lt|b|=|d|\lt|a|$，故绝对值最大的是$a$。

4.(2023·涟水县期末·知识点3·能力点1)化简:
(1)-|-3|;(2)-|-(-7.5)|;
(3)+|-(+7)|;(4)|-(+1/2)|。

答案： 解：
(1)$-|-3|=-3$。
(2)$-|-(-7.5)|=-7.5$。
(3)$|+(-7)|=7$。
(4)$\left|-\left(+\frac{1}{2}\right)\right|=\frac{1}{2}$。

5.(知识点1,2·能力点1)下列各组数中,互为相反数的是( )。

A.+1与|-1|
B.+(+7)与-(-7)
C.+(-3)与-|+3|
D.-|-4|与-(-4)

答案： D 【解析】$|-1|=1=+1$，所以$+1$与$|-1|$相等，不互为相反数，故 A 选项不符合题意；$+(+7)=7$，$-(-7)=7$，所以$+(+7)$与$-(-7)$相等，不互为相反数，故 B 选项不符合题意；$+(-3)=-3$，$-|+3|=-3$，所以$+(-3)$与$-|+3|$相等，不互为相反数，故 C 选项不符合题意；$-|-4|=-4$，$-(-4)=4$，所以$-|-4|$与$-(-4)$互为相反数，故 D 选项符合题意。故选 D。

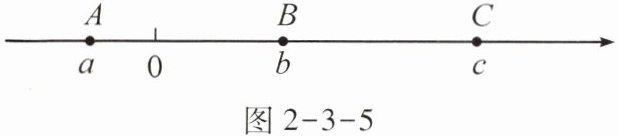
6.(2023·洛川县期末·能力点3)如图2-3-5,A,B,C三点所表示的有理数分别为a,b,c,则-a,b,-c的大小关系为 。(用"＜"连接)

答案：
$-c\lt -a\lt b$ 【解析】$-a$，$-c$在数轴上的对应点的位置如图，因为数轴上左边的数总是小于右边的数，所以由数轴可知$-c\lt -a\lt b$。

7.(2023·建邺区期末·知识点2·能力点3)如图2-3-6,数轴上有3个点,它们所表示的数分别为a,b,c。
(1)在数轴上标出a,b,c的相反数-a,-b,-c;
(2)把a,b,c和它们的相反数用"＜"连接起来;
(3)如果将表示数a的点向左移动3个单位长度,同时将表示数b的点向右移动4个单位长度,表示数c的点保持在原来的位置,则移动后的a,b,c三个数的大小关系如何?

答案：
解：
(1)在数轴上标出$-a$，$-b$，$-c$，如图①。
(2)由
(1)中的数轴可得出$-a\lt b\lt -c\lt c\lt -b\lt a$。
(3)如图②，根据题意标出数$a$，$b$移动后的数$a'$，$b'$的位置， 根据数轴得出$a'\lt c\lt b'$，即移动后的$a$，$b$，$c$三个数的大小关系为$a\lt c\lt b$。