第61页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
12. (2024·广西)如图,壮壮同学投掷实心球,出手(点 $ P $ 处)的高度 $ OP $ 是 $ \frac{7}{4} $ m,出手后实心球沿一段抛物线运行,到达最高点时,水平距离是 5 m,高度是 4 m.若实心球落地点为 $ M $,则 $ OM = $

$\frac{35}{3}$
m.
答案:
12.$\frac{35}{3}$
13. 新考向 真实情境(2024·南宁武鸣区期中)江南的丝绸以其质地细腻、工艺精湛而闻名.现有一种丝绸制成的丝巾,每条成本 50 元,出于营销考虑,要求每条丝巾的售价不低于 60 元且不高于 110 元,销售一段时间发现,每天的销售数量 $ y $(条)与销售单价 $ x $(元)满足一次函数关系,部分数据如下表所示:
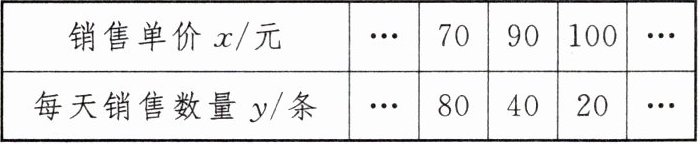
(1)请求出 $ y $ 与 $ x $ 的函数解析式.
(2)设该店每天销售丝巾所获得的利润为 $ w $ 元,写出 $ w $ 与 $ x $ 的函数解析式.
(3)将该商品销售的单价定为多少元时,才能使得当天所获利润最大?最大利润是多少元?

(1)请求出 $ y $ 与 $ x $ 的函数解析式.
(2)设该店每天销售丝巾所获得的利润为 $ w $ 元,写出 $ w $ 与 $ x $ 的函数解析式.
(3)将该商品销售的单价定为多少元时,才能使得当天所获利润最大?最大利润是多少元?
答案:
13.
(1)y = -2x + 220(60 ≤ x ≤ 110)。
(2)w = -2x² + 320x - 11000。
(3)将该商品销售的单价定为80元时,才能使得当天所获利润最大,最大利润是1800元。
(1)y = -2x + 220(60 ≤ x ≤ 110)。
(2)w = -2x² + 320x - 11000。
(3)将该商品销售的单价定为80元时,才能使得当天所获利润最大,最大利润是1800元。
14. 新考向 跨学科(2024·柳州十五中模拟)某物理兴趣小组对一款饮水机的工作电路展开研究,如图 1,将变阻器 $ R $ 的滑片从一端滑到另一端,绘制出变阻器 $ R $ 消耗的电功率 $ P $ 随电流 $ I $ 变化的关系图象,如图 2 所示,且该图象是经过原点的一条抛物线的一部分,则变阻器 $ R $ 消耗的电功率 $ P $ 最大为(
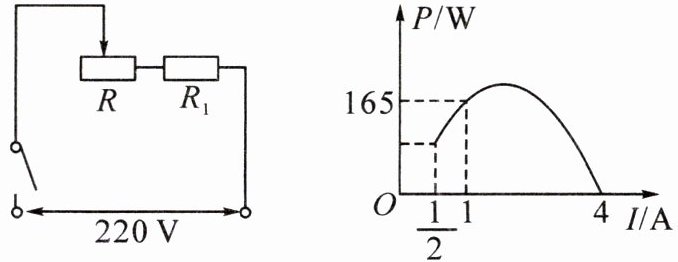
A.$ 160 $ W
B.$ 180 $ W
C.$ 200 $ W
D.$ 220 $ W
D
)
A.$ 160 $ W
B.$ 180 $ W
C.$ 200 $ W
D.$ 220 $ W
答案:
14.D
15. 新考向 传统文化如图,剪纸艺术是中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,以这个蝴蝶图案的对称轴为 $ y $ 轴建立平面直角坐标系,图中点 $ E $,$ F $ 关于 $ y $ 轴对称,其中点 $ E $ 的坐标为 $ (3n - 4,m + 1) $,点 $ F $ 的坐标为 $ (n^2,2m) $.若点 $ E $ 到 $ x $ 轴的距离小于它到 $ y $ 轴的距离,则二次函数 $ y = x^2 + nx + m $ 图象的顶点坐标是(
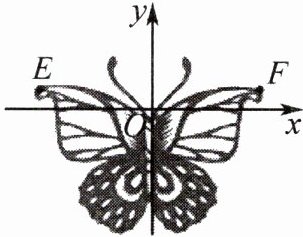
A.$ (-2,-3) $
B.$ (2,-3) $
C.$ (-\frac{1}{2},\frac{3}{4}) $
D.$ (-\frac{1}{2},\frac{3}{4}) $ 或 $ (2,-3) $
B
)
A.$ (-2,-3) $
B.$ (2,-3) $
C.$ (-\frac{1}{2},\frac{3}{4}) $
D.$ (-\frac{1}{2},\frac{3}{4}) $ 或 $ (2,-3) $
答案:
15.B
16. 新考向 新定义问题(2024·南宁三中期中)新定义:$[a,b,c]$ 为二次函数 $ y = ax^2 + bx + c(a \neq 0,a,b,c $ 为实数)的“图象数”.例如:$ y = x^2 - 2x + 3 $ 的“图象数”为 $ [1,-2,3] $.若“图象数”是 $ [m,2m - 4,2m + 4] $ 的二次函数的图象与 $ x $ 轴只有一个交点,则 $ m $ 的值为
2$\sqrt 5$ - 4 或 -2$\sqrt 5$ - 4
.
答案:
16.2$\sqrt 5$ - 4 或 -2$\sqrt 5$ - 4
查看更多完整答案,请扫码查看


