第104页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
1. 一个正多边形的中心角为 $30^{\circ}$,这个正多边形的边数是(
A.3
B.6
C.8
D.12
D
)A.3
B.6
C.8
D.12
答案:
1.D
2. 如图,正五边形 $ABCDE$ 内接于 $\odot O$,连接 $OC$,$OD$,则 $\angle COD =$(
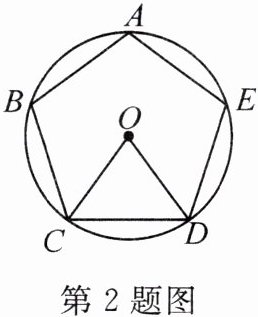
A.$72^{\circ}$
B.$60^{\circ}$
C.$54^{\circ}$
D.$48^{\circ}$
A
)
A.$72^{\circ}$
B.$60^{\circ}$
C.$54^{\circ}$
D.$48^{\circ}$
答案:
2.A
3. (2024·甘孜州)如图,正六边形 $ABCDEF$ 内接于 $\odot O$,$OA = 1$,则 $AB$ 的长为(
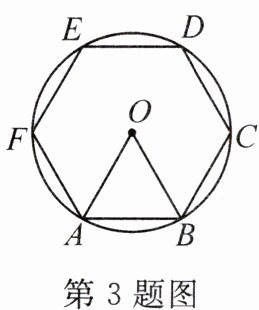
A.2
B.$\sqrt{3}$
C.1
D.$\frac{1}{2}$
C
)
A.2
B.$\sqrt{3}$
C.1
D.$\frac{1}{2}$
答案:
3.C
4. 在半径为 5 的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为
5$\sqrt{2}$
。
答案:
4.5$\sqrt{2}$
5. 如图,$\odot O$ 的内接正三角形 $ABC$ 的边心距 $OD$ 为 $2\mathrm{cm}$,则 $\odot O$ 的半径为
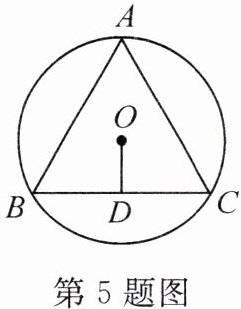
4
$\mathrm{cm}$。
答案:
5.4
6. (2024·镇江)如图,$AB$ 是 $\odot O$ 的内接正 $n$ 边形的一边,点 $C$ 在 $\odot O$ 上,$\angle ACB = 18^{\circ}$,则 $n =$
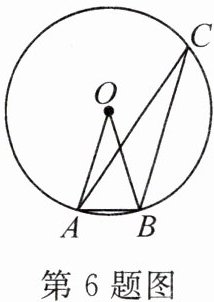
10
。
答案:
6.10
7. 如图,点 $O$ 是正八边形 $A_1A_2\cdots A_8$ 外接圆的圆心,连接 $A_4A_6$。若 $\odot O$ 的半径为 $4\mathrm{cm}$,则 $A_4A_6 =$
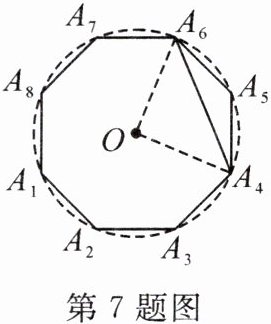
4$\sqrt{2}$
$\mathrm{cm}$。
答案:
7.4$\sqrt{2}$
8. (2024·南宁翠竹实验学校月考)正六边形的边长为 2,则边心距为
$\sqrt{3}$
。
答案:
8.$\sqrt{3}$
9. 新考向 真实情境(教材九上 P108 习题 T5 变式)如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 $b = 3\mathrm{cm}$,则螺帽边长 $a =$
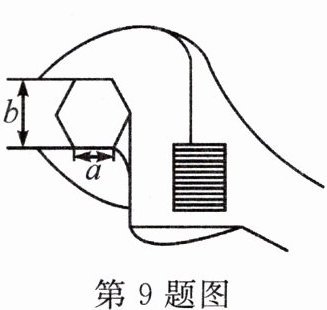
$\sqrt{3}$cm
。
答案:
9.$\sqrt{3}$cm
10. 如图,$\odot O$ 的半径为 $R$,六边形 $ABCDEF$ 是圆内接正六边形,四边形 $EFGH$ 是正方形。
(1)求 $\angle OGF$ 的度数。
(2)求正六边形与正方形的面积比。
 ]
]
(1)求 $\angle OGF$ 的度数。
(2)求正六边形与正方形的面积比。
 ]
]
答案:
10.解:
(1)
∵$\angle OFE=60^{\circ}$,$\angle EFG=90^{\circ}$,
∴$\angle OFG=150^{\circ}$.
∵$OF=EF=FG$,
∴$\angle OGF=\frac{180^{\circ}-\angle OFG}{2}=15^{\circ}$.
(2)$S_{正六边形}=6× \frac{1}{2}× R× \frac{\sqrt{3}}{2}R=\frac{3\sqrt{3}}{2}R^{2}$,$S_{正方形}=R^{2}$,
∴$\frac{S_{正六边形}}{S_{正方形}}=\frac{\frac{3\sqrt{3}}{2}R^{2}}{R^{2}}=\frac{3\sqrt{3}}{2}$.
(1)
∵$\angle OFE=60^{\circ}$,$\angle EFG=90^{\circ}$,
∴$\angle OFG=150^{\circ}$.
∵$OF=EF=FG$,
∴$\angle OGF=\frac{180^{\circ}-\angle OFG}{2}=15^{\circ}$.
(2)$S_{正六边形}=6× \frac{1}{2}× R× \frac{\sqrt{3}}{2}R=\frac{3\sqrt{3}}{2}R^{2}$,$S_{正方形}=R^{2}$,
∴$\frac{S_{正六边形}}{S_{正方形}}=\frac{\frac{3\sqrt{3}}{2}R^{2}}{R^{2}}=\frac{3\sqrt{3}}{2}$.
11. 新考向 几何直观 图 1 是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形。
如图 2,$AE$ 是 $\odot O$ 的直径,用直尺和圆规作 $\odot O$ 内接正八边形 $ABCDEFGH$(不写作法,保留作图痕迹)。
]
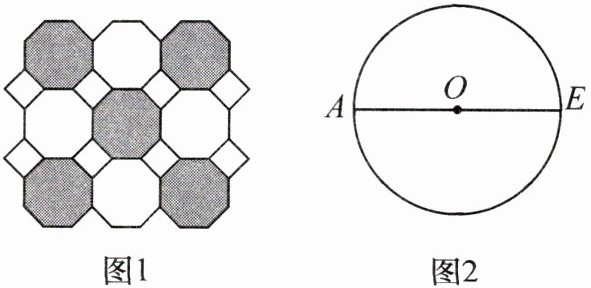
如图 2,$AE$ 是 $\odot O$ 的直径,用直尺和圆规作 $\odot O$ 内接正八边形 $ABCDEFGH$(不写作法,保留作图痕迹)。
]

答案:
11.解:如图所示
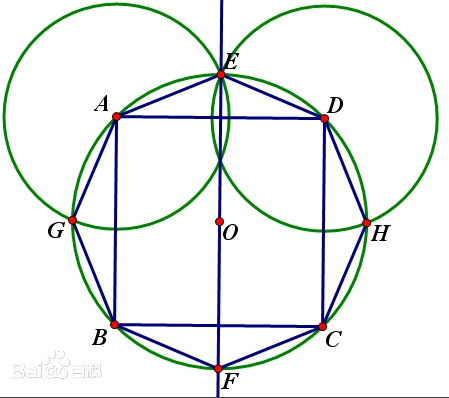
11.解:如图所示

查看更多完整答案,请扫码查看


