第141页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
8. 新考向 跨学科 已知电灯电路两端的电压 $ U $ 为 $ 220 V $,通过灯泡的电流强度 $ I(A) $ 的最大限度不得超过 $ 0.11 A $。设选用灯泡的电阻为 $ R(\Omega) $,下列说法正确的是(
A.$ R $ 至少为 $ 2000 \Omega $
B.$ R $ 至多为 $ 2000 \Omega $
C.$ R $ 至少为 $ 24.2 \Omega $
D.$ R $ 至多为 $ 24.2 \Omega $
A
)A.$ R $ 至少为 $ 2000 \Omega $
B.$ R $ 至多为 $ 2000 \Omega $
C.$ R $ 至少为 $ 24.2 \Omega $
D.$ R $ 至多为 $ 24.2 \Omega $
答案:
8.A
9. 如图,这是某公园“水上滑梯”的侧面图,其中 $ BC $ 段可看成是一段双曲线,建立如图所示的平面直角坐标系,其中,矩形 $ AOE B $ 为向上攀爬的梯子,$ OA = 5 $ 米,进口 $ AB // OD $,且 $ AB = 2 $ 米,出口点 $ C $ 距水面的距离 $ CD $ 为 $ 1 $ 米,则 $ B $,$ C $ 之间的水平距离 $ DE $ 为
8
米。
答案:
9.8
10. 新考向 综合与实践 实验与探究
如图 1,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘 $ A $ 中放置一个重物,在右边活动托盘 $ B $ (可左右移动) 中放置一定质量的砝码,使得仪器左右保持平衡。改变活动托盘 $ B $ 与点 $ O $ 的距离 $ x(cm) $,观察活动托盘 $ B $ 中砝码的质量 $ y(g) $ 的变化情况。实验数据记录如下表:
【初步尝试】
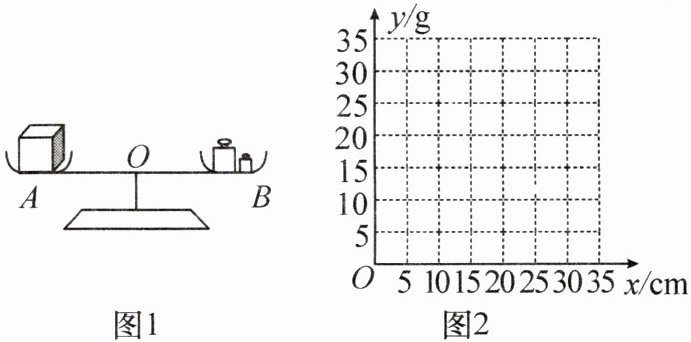
(1) 把表中 $ (x,y) $ 的各组对应值作为点的坐标,在图 2 的平面直角坐标系中描出相应的点,用平滑曲线连接这些点。
【观察猜想】
(2) 观察所画的图象,猜测 $ y $ 与 $ x $ 之间的函数关系,求出函数关系式。
【灵活运用】
(3) 当砝码的质量为 $ 24 g $ 时,活动托盘 $ B $ 与点 $ O $ 的距离是
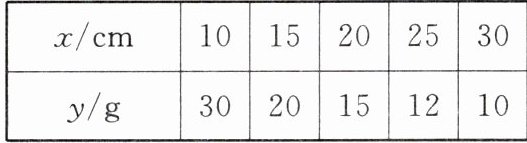
如图 1,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘 $ A $ 中放置一个重物,在右边活动托盘 $ B $ (可左右移动) 中放置一定质量的砝码,使得仪器左右保持平衡。改变活动托盘 $ B $ 与点 $ O $ 的距离 $ x(cm) $,观察活动托盘 $ B $ 中砝码的质量 $ y(g) $ 的变化情况。实验数据记录如下表:
【初步尝试】
(1) 把表中 $ (x,y) $ 的各组对应值作为点的坐标,在图 2 的平面直角坐标系中描出相应的点,用平滑曲线连接这些点。
【观察猜想】
(2) 观察所画的图象,猜测 $ y $ 与 $ x $ 之间的函数关系,求出函数关系式。
【灵活运用】
(3) 当砝码的质量为 $ 24 g $ 时,活动托盘 $ B $ 与点 $ O $ 的距离是
12.5
$ cm $。

答案:
10.
(1)如图所示
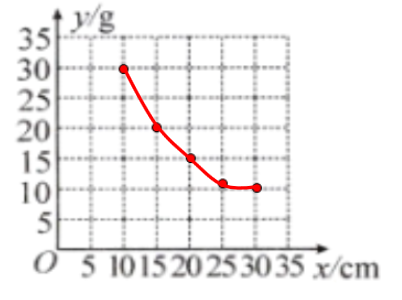
(2)由图象猜测y与x之间的函数关系为反比例函数,$\therefore$设y与x之间的函数关系式为$y=\frac{k}{x}(k\neq0),$把x=10,y=30代入,得k=300,$\therefore y=\frac{300}{x}。$将其余各点代入验证均适合,$\therefore y$与x的函数关系式为$y=\frac{300}{x}。$
(3)12.5
10.
(1)如图所示

(2)由图象猜测y与x之间的函数关系为反比例函数,$\therefore$设y与x之间的函数关系式为$y=\frac{k}{x}(k\neq0),$把x=10,y=30代入,得k=300,$\therefore y=\frac{300}{x}。$将其余各点代入验证均适合,$\therefore y$与x的函数关系式为$y=\frac{300}{x}。$
(3)12.5
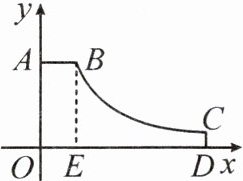
11. 新考向 真实情境 (2023·河池凤山县期末) 我校的饮水机接通电源就进入自动程序,开机加热时每分钟上升 $ 10^{\circ} C $,加热到 $ 100^{\circ} C $,停止加热,水温开始下降,此时水温 $ (^{\circ} C) $ 与开机后用时 $ (min) $ 成反比例关系. 直至水温降至 $ 20^{\circ} C $ 时自动开机加热,重复上述自动程序. 若在水温为 $ 20^{\circ} C $ 时,接通电源后,水温 $ y(^{\circ} C) $ 和时间 $ x(min) $ 的关系如图所示.
(1) $ a = $
(2) 直接写出图中 $ y $ 关于 $ x $ 的函数解析式。
(3) 饮水机有多少时间能使水温保持在 $ 50^{\circ} C $ 及以上?
(4) 若某天上午 $ 7:00 $ 饮水机自动接通电源,开机温度正好是 $ 20^{\circ} C $,则学生上午第一节下课时 $ (8:40) $ 能喝到 $ 50^{\circ} C $ 以上的水吗?请说明理由。
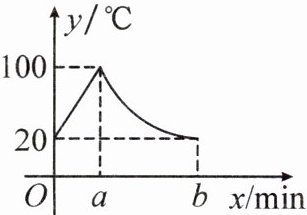
(1) $ a = $
8
,$ b = $40
。(2) 直接写出图中 $ y $ 关于 $ x $ 的函数解析式。
(3) 饮水机有多少时间能使水温保持在 $ 50^{\circ} C $ 及以上?
(4) 若某天上午 $ 7:00 $ 饮水机自动接通电源,开机温度正好是 $ 20^{\circ} C $,则学生上午第一节下课时 $ (8:40) $ 能喝到 $ 50^{\circ} C $ 以上的水吗?请说明理由。

答案:
11.
(1)8 40
(2)由图可得,$y=\begin{cases}10x + 20(0\leq x\leq8),\frac{800}{x}(8<x\leq40).\end{cases} (3)$在$y=10x + 20(0\leq x\leq8)$中,令y=50,解得x=3;在$y=\frac{800}{x}$中,令y=50,解得x=16。$\therefore$饮水机使水温保持在50℃及以上的时间有16 - 3 = 13(min)。
(4)由题意可知,饮水机工作时40min为一个循环,上午7:00到上午第一节下课时(8:40)的时间是100min,是2个40min多20min,$\therefore\frac{800}{20}=40(℃)。$答:学生上午第一节下课时(8:40)不能喝到50℃以上的水。
(1)8 40
(2)由图可得,$y=\begin{cases}10x + 20(0\leq x\leq8),\frac{800}{x}(8<x\leq40).\end{cases} (3)$在$y=10x + 20(0\leq x\leq8)$中,令y=50,解得x=3;在$y=\frac{800}{x}$中,令y=50,解得x=16。$\therefore$饮水机使水温保持在50℃及以上的时间有16 - 3 = 13(min)。
(4)由题意可知,饮水机工作时40min为一个循环,上午7:00到上午第一节下课时(8:40)的时间是100min,是2个40min多20min,$\therefore\frac{800}{20}=40(℃)。$答:学生上午第一节下课时(8:40)不能喝到50℃以上的水。
查看更多完整答案,请扫码查看


