《2025年名校课堂九年级数学全一册人教版广西专版》

11. (2024·南宁五一路学校月考改编)某校八年级(1)(2)班准备集体购买一种T恤衫参加一项社会活动.了解到某商店正好有这种T恤衫的促销,当购买10件时每件140元,购买数量每增加1件单价减少1元;当购买数量为60件(含60件)以上时,一律每件80元.
(1)如果购买x件$(10＜x＜60)$,每件的单价为y元,请写出y关于x的函数关系式.
(2)如果八年级(1)(2)班共购买了100件T恤衫,由于某种原因需分两批购买,且第一批购买数量多于30件且不多于40件.已知购买两批T恤衫一共花了9200元,求第一批T恤衫的购买数量.

答案： 11.解：
(1)由题意，得$y = 140-(x - 10)=150 - x(10＜x＜60)$。
(2)设第一批购买$x$件，则第二批购买$(100 - x)$件。当$30＜x\leq40$时，$60\leq100 - x＜70$，则$x(150 - x)+80(100 - x)=9200$，解得$x_1=30$(不合题意，舍去)，$x_2=40$。答：第一批T恤衫的购买数量为40件。

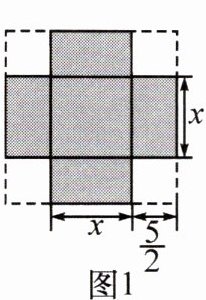
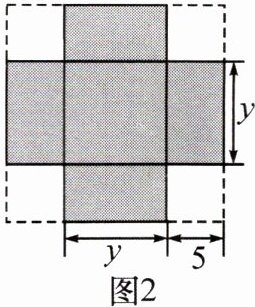
12. 新考向 传统文化(2024·南宁三中期中)清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如$x^{2}+10x=56$的方程,求正数解的几何方法如下:“如图1,先构造一个面积为$x^{2}$的正方形,再以该正方形的边长为一边向外构造四个面积均为$\frac{5}{2}x$的矩形,则大正方形的面积为$56+25=81$,则原方程的正数解为$9-5=4$.”小聪按此方法解关于y的方程$y^{2}+20y+m=0$时,构造出如图2所示的图形,已知阴影部分的面积为156,则该方程的正数解为 (A)

A.$y=6$
B.$y=8$
C.$y=16$
D.$y=2\sqrt{39}-5$

答案： 12.A

13. 新考向 阅读理解(2024·南宁四十七中开学考)阅读与思考:
【知识理解】
小悦同学解一元二次方程的方法如下所示,请完成相应的任务.
利用均值换元法解一类一元二次方程:
解方程:$(200+x)(64-\frac{x}{10})=14400$.
第一步:原方程可变形为$(x+200)(x-640)=-144000$;
第二步:令$t=\frac{(x+200)+(x-640)}{2}=x-220$;
第三步:第一步的方程可变形为$(t+420)(t-420)=-144000$;
第四步:……
根据t的值可以求出$x_{1}=400,x_{2}=40$.
方法总结:
求第一步方程等号左边两个多项式的平均值,从而换元得到较为简单的一元二次方程,因此,这种方法称为均值换元法.我们在解决形如$(ax+c)(ax+b)=d$(其中a,b,c,d是常数,且$a\neq 0$)的方程时可以利用均值换元法求解.
(1)利用均值换元法解方程体现的数学思想是C.
A. 分类讨论思想
B. 数形结合思想
C. 整体代换思想
D. 类比思想
(2)完成材料中第三步以后求t值的过程.
【知识迁移】
(3)根据材料内容,利用均值换元法解方程:$(x+30)(11-\frac{x}{10})=130$.

答案： 13.解：
(1)C
(2)$\because t^{2}-176400=-144000$。$\therefore t^{2}=32400$，解得$t=\pm180$。$\therefore x - 220 = 180$或$x - 220=-180$，解得$x_1=400$，$x_2=40$。
(3)整理，得$(x + 30)(x - 110)=-1300$。令$t=\frac{x + 30+x - 110}{2}=x - 40$，则原方程可变形为$(t + 70)(t - 70)=-1300$。$\therefore t^{2}-4900=-1300$。$\therefore t=\pm60$。$\therefore x - 40 = 60$或$x - 40=-60$，解得$x_1=100$，$x_2=-20$。