第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
23. (8分)把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
|颜色|红|黄|蓝|白|紫|绿|
|花的朵数|1|2|3|4|5|6|
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.该长方体的下底面共有多少朵花?

|颜色|红|黄|蓝|白|紫|绿|
|花的朵数|1|2|3|4|5|6|
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.该长方体的下底面共有多少朵花?

答案:
因为四个正方体的颜色、花朵分布完全相同,所以根据题图,得红色面对绿色面,黄色面对紫色面,蓝色面对白色面,所以可知长方体下底面从左到右依次是紫色、黄色、绿色、白色,所以该长方体的下底面共有$5+2+6+4=17$(朵)花.
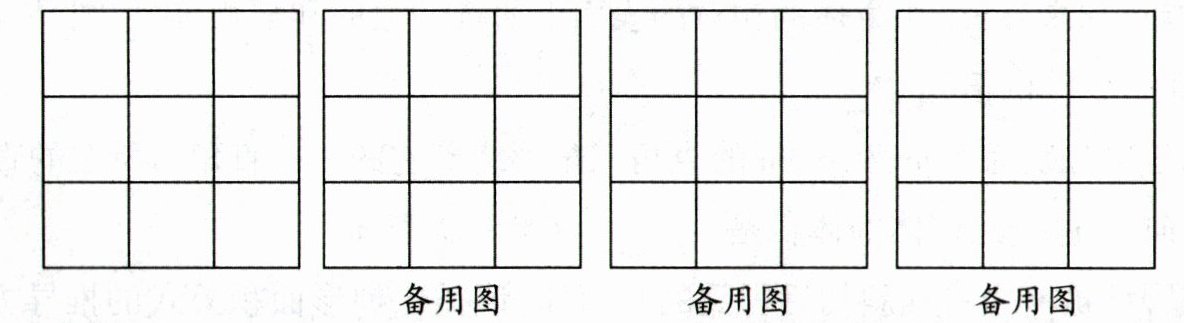
24. (10分)如图,一个棱长为10cm的无盖正方体可以展开成下面的平面图形.
(1)这个表面展开图的面积是____$cm^{2}$.
(2)你还能在下面小方格中画出无盖正方体的其他不同形状的表面展开图吗?请画出可能的情形(把需要的小正方形涂上阴影).

(3)将一个无盖正方体展开成如图平面图形的过程中,需要剪开____条棱.
A. 3 B. 4 C. 5 D. 不确定
(1)这个表面展开图的面积是____$cm^{2}$.
(2)你还能在下面小方格中画出无盖正方体的其他不同形状的表面展开图吗?请画出可能的情形(把需要的小正方形涂上阴影).

(3)将一个无盖正方体展开成如图平面图形的过程中,需要剪开____条棱.
A. 3 B. 4 C. 5 D. 不确定

答案:
(1)500 【解析】$5×10^{2}=500(\text{cm}^2)$.
(2)如图所示.(合理即可)
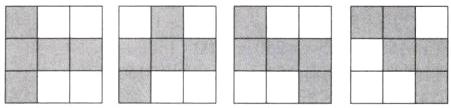
(3)B 【解析】根据题意可得将一个无盖正方体展开成如题图平面图形的过程中,需要剪开4条棱.
(1)500 【解析】$5×10^{2}=500(\text{cm}^2)$.
(2)如图所示.(合理即可)

(3)B 【解析】根据题意可得将一个无盖正方体展开成如题图平面图形的过程中,需要剪开4条棱.
25. (10分)下列图形中,图①是正方体木块,把它切去一块,得到如图②③④⑤的木块.

(1)图①②的相关数据已经给出,请你将图③④⑤中木块的顶点数、棱数、面数填入表中:
|图号|顶点数x|棱数y|面数z|
|①|8|12|6|
|②|6|9|5|
|③| | | |
|④| | | |
|⑤| | | |
(2)如表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数、棱数、面数之间的数量关系式.

(1)图①②的相关数据已经给出,请你将图③④⑤中木块的顶点数、棱数、面数填入表中:
|图号|顶点数x|棱数y|面数z|
|①|8|12|6|
|②|6|9|5|
|③| | | |
|④| | | |
|⑤| | | |
(2)如表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数、棱数、面数之间的数量关系式.
答案:
(1)如表:
|图号|顶点数x|棱数y|面数z|
|①|8|12|6|
|②|6|9|5|
|③|8|12|6|
|④|8|13|7|
|⑤|10|15|7|
(2)观察上表可得:$12=8+6-2$,$9=6+5-2$,$13=8+7-2$,$15=10+7-2$,所以$y=x+z-2$,所以顶点数x、棱数y、面数z之间的数量关系式为$y=x+z-2$.
(1)如表:
|图号|顶点数x|棱数y|面数z|
|①|8|12|6|
|②|6|9|5|
|③|8|12|6|
|④|8|13|7|
|⑤|10|15|7|
(2)观察上表可得:$12=8+6-2$,$9=6+5-2$,$13=8+7-2$,$15=10+7-2$,所以$y=x+z-2$,所以顶点数x、棱数y、面数z之间的数量关系式为$y=x+z-2$.
查看更多完整答案,请扫码查看


