《2025年学霸提优大试卷七年级数学上册苏科版》

7. 如图,$ C,D $ 是线段 $ AB $ 上的两点,且 $ AC = \frac{1}{3}CD = \frac{1}{4}DB $.已知图中所有线段长度之和为81,则 $ CD $ 的长为 (A)
A.9
B.$ \frac{243}{8} $
C.$ \frac{243}{16} $
D.以上都不对

答案： A

8. 如图,已知直线 $ AB,CD $ 被直线 $ AC $ 所截,$ AB // CD $,$ E $ 是 $ CD $ 上方的一点(点 $ E $ 不在直线 $ AB,AC $ 上).设 $ \angle BAE = \alpha $,$ \angle DCE = \beta $,下列各式:①$ \alpha + \beta $;②$ \alpha - \beta $;③$ \beta - \alpha $;④$ 180^{\circ} - \alpha - \beta $;⑤$ 360^{\circ} - \alpha - \beta $.$ \angle AEC $ 的度数可能是 (D)
A.①②④
B.①③⑤
C.②③④⑤
D.①②③④⑤

答案： D

9. 如图,想在河的两岸搭建一座桥,搭建方式最短的是 $ PM $,理由是垂线段最短.

答案： 垂线段最短

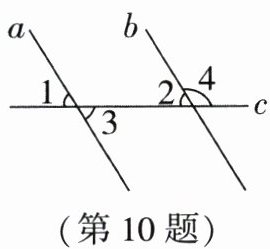
10. (2024·苏州期中)如图,直线 $ a,b $ 被直线 $ c $ 所截,添加一个条件∠2=∠3(答案不唯一),使 $ a // b $.

答案： ∠2=∠3(答案不唯一)

11. 已知 $ \angle \alpha = 25^{\circ}15' $,$ \angle \beta = 25.15^{\circ} $,则 $ \angle \alpha $＞$ \angle \beta $.(填“$ ＞ $”“$ ＜ $”或“$ = $”)

答案： ＞

12. (2024·宿迁校级期中)从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成5个三角形.

答案： 5

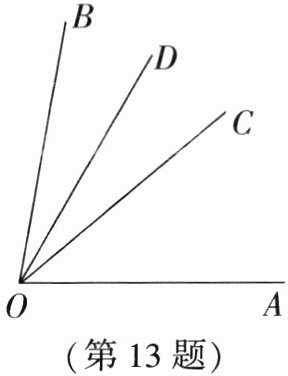
13. (2025·南京模拟)如图,$ OC $ 是 $ \angle AOB $ 的平分线,$ OD $ 是 $ \angle COB $ 的平分线,$ \angle AOD = 60^{\circ} $,则 $ \angle AOB = $80$ ^{\circ} $.

答案： 80

14. 如图,线段 $ AD = 16 $,长度为2的线段 $ BC $ 在线段 $ AD $ 上运动,分别取线段 $ AC,BD $ 的中点 $ M,N $,则 $ MN = $7.

答案： 7

15. 某校下午放学时间是 $ 5:45 $,此时时针与分针的夹角(较小角)为97.5°.

答案： 97.5°