《2025年学霸提优大试卷七年级数学上册苏科版》

13. (2024·宿迁宿城区期末)若有理数a,b满足等式$|b - a|-|a + b| = 2b$,则有理数a,b在数轴上的位置可能是(D)

答案： D 【解析】若|b - a| - |a + b| = 2b,则b - a + a + b = 2b,所以b ＞ a且a + b ＜ 0.故选D.

14. (2024·苏州工业园区期末)三边都相等的三角形叫作等边三角形.如图,将数轴从点A开始向右折出一个等边三角形ABC,点A,B,C表示的数分别为$2x - 7$,$x - 3$,$4 - x$.现将等边三角形ABC向右滚动,则与表示数2024的点重合的点(A)
A.是点A
B.是点B
C.是点C
D.不存在
]

答案： A A 【解析】由题意可得(2x - 7) - (x - 3) = (x - 3) - (4 - x),解得x = 3.所以A表示 - 1,B表示0,C表示1,所以等边三角形的边长为1,所以数2024对应的点与1的距离为2024 - 1 = 2023,2023÷3 = 674……1,所以从C点出发到数2024对应的点滚动了674周多一边.所以数2024的对应点与等边三角形的点A重合.故选A.

15. 现有1张大长方形和3张相同的小长方形卡片,按如图所示两种方式摆放,则小长方形的长与宽的差是(C)
A.$a - b$
B.$\frac{a - b}{2}$
C.$\frac{a - b}{3}$
D.$\frac{a + b}{3}$
]

答案： C 【解析】设小长方形的长为x、宽为y,大长方形的长为m,则a + 2y = x + m,2x + b = y + m.所以x = a + 2y - m,y = 2x + b - m,所以x - y = (a + 2y - m) - (2x + b - m).即x - y = a + 2y - m - 2x - b + m,3x - 3y = a - b,所以$x - y=\frac{a - b}{3}$.即小长方形的长与宽的差是$\frac{a - b}{3}$.故选C.

16. (2024·扬州校级期末)将一张正方形纸片ABCD按如图所示的方式折叠,CE,CF为折痕,点B,D折叠后的对应点分别为$B'$,$D'$,若$∠ECF = 22^{\circ}$,则$∠B'CD'$的度数为(B)
A.$48^{\circ}$
B.$46^{\circ}$
C.$44^{\circ}$
D.$42^{\circ}$

答案： B 【解析】由折叠的性质可得$∠BCF = ∠B'CF=\frac{1}{2}∠BCB'$,$∠DCE = ∠D'CE=\frac{1}{2}∠DCD'$.因为纸片ABCD是正方形,所以∠BCD = 90°.设$∠D'CF = α$,$∠B'CE = β$,则$∠D'CE = ∠ECF + ∠D'CF = 22^{\circ}+α$,$∠B'CF = ∠ECF + ∠B'CE = 22^{\circ}+β$,$∠BCB' = 2∠B'CF = 2(22^{\circ}+β)$,$∠DCD' = 2∠D'CE = 2(22^{\circ}+α)$.$∠BCD' = 90^{\circ}-∠DCD' = 90^{\circ}-2(22^{\circ}+α)$,$∠DCB' = 90^{\circ}-∠BCB' = 90^{\circ}-2(22^{\circ}+β)$,$∠B'CD' = ∠D'CF + ∠ECF + ∠B'CE = α + 22^{\circ}+β$.令$∠B'CD' = α + β + 22^{\circ}= θ$,因为$∠B'CD' = 90^{\circ}-(∠BCD'+∠DCB')$,所以$α + 22^{\circ}+β = 90^{\circ}-[90^{\circ}-2(22^{\circ}+α)]-[90^{\circ}-2(22^{\circ}+β)]$,整理可得$α + 22^{\circ}+β = 2(α + 22^{\circ}+β)-46^{\circ}$,即θ = 2θ - 46°,解得θ = 46°.所以$∠B'CD' = θ = 46^{\circ}$.故选B.

17. 如图,在数轴上,O为原点,点A对应的数为2,点B对应的数为-12.在数轴上有两动点C和D,它们同时向右运动,点C从点A出发,速度为每秒4个单位长度,点D从点B出发,速度为每秒6个单位长度,设运动时间为t秒,当点O,C,D中,其中一点正好位于另外两点所确定线段的中点时,t的值为1或$\frac{13}{4}$.

答案： 1或$\frac{13}{4}$ 【解析】由题意得点C表示的数是2 + 4t,点D表示的值是 - 12 + 6t.当O是CD中点时,依题意有2 + 4t - 12 + 6t = 2×0,解得t = 1.当D是OC中点时,依题意有2 + 4t + 0 = 2×(- 12 + 6t),解得$t=\frac{13}{4}$.当C是OD中点时,依题意有 - 12 + 6t + 0 = 2×(2 + 4t),解得t = -8(舍去).故t的值为1或$\frac{13}{4}$.

18. (2024·盐城大丰区期末)如图①,一款暗插销由外壳AB、开关CD、锁芯DE三部分组成,其工作原理如图②,开关CD绕固定点O转动,由连接点D带动锁芯DE移动.图③为插销开启状态,此时连接点D在线段AB上,如$D_{1}$位置.开关CD绕点O顺时针旋转$180^{\circ}后得到C_{2}D_{2}$,锁芯弹回至$D_{2}E_{2}$位置(点B与点$E_{2}$重合),如图④此时插销闭合.已知$CD = 72mm$,$AD_{2}-AC_{1} = 50mm$,则$BE_{1} = $______mm.
]

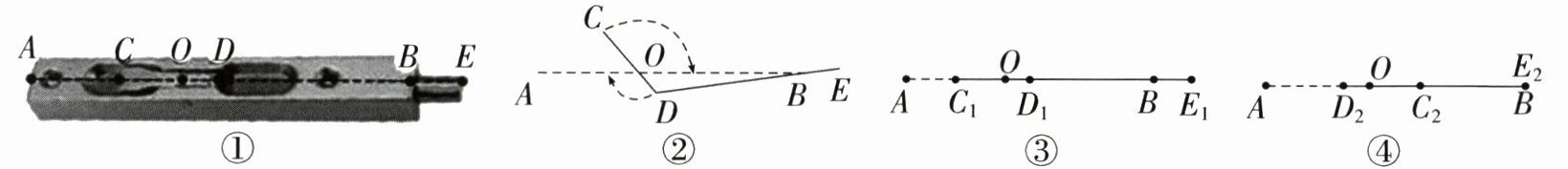
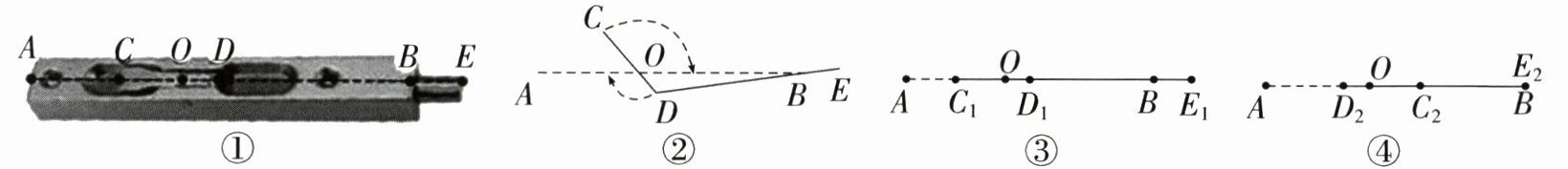
22

答案： 22 【解析】由题图③得当点D在O的右侧时,即$D_{1}$位置时,B与点E的距离为$BE_{1}$,由题图④得当点D在O的左侧时,即$D_{2}$位置时,B与点E重合,即$E_{2}$位置,所以$BE_{1}=OD_{1}+OD_{2}=2OD_{2}$.因为$AD_{2}-AC_{1}=50\ \text{mm}$,所以$(AO - OD_{2})-(AO - OC_{1})=50\ \text{mm}$,所以$OC_{1}-OD_{2}=50\ \text{mm}$,所以$OC_{1}=(OD_{2}+50)\ \text{mm}$.因为CD = OC + OD = $OC_{1}+OD_{2}$,所以CD = $OC_{1}+OD_{2}=OD_{2}+50+OD_{2}=72\ \text{mm}$,所以$2OD_{2}=22\ \text{mm}$,所以$BE_{1}=22\ \text{mm}$.