《2025年学霸提优大试卷七年级数学上册苏科版》

16. 如图,$AD // CE$,$∠ABC = 100^{\circ}$,则$∠2 - ∠1$的度数是______.

答案：
80° [解析]如图，作BF//AD,因为AD//CE,所以AD//BF//EC,所以∠1=∠3,∠4+∠2=180°，∠3+∠4=100°，所以∠1+∠4=100°，∠2+∠4=180°，所以∠2−∠1=80°.

17. 已知:在同一平面内,线段$AB$的长为 6,点$A$,$B到直线l$的距离分别为 2 和 3,则符合条件的直线$l$共有______条.

答案：
4 [解析]如图.符合条件的直线l共有4条.

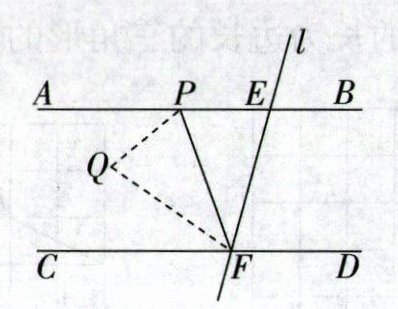
18. 如图,直线$AB // CD$,直线$l与直线AB$,$CD相交与点E$,$F$,$P是射线EA$上的一个动点(不包括端点$E$),将$△EPF沿PF$折叠,使顶点$E落在点Q$处,若$∠PEF = 75^{\circ}$,$∠CFQ = \frac{1}{2}∠PFC$.则$∠EFP$的度数为______.

答案：
35°或63° [解析]分两种情况：如图①,当点Q在平行线AB,CD之间时，设∠PFQ=x,由折叠可得∠EFP=x,因为∠CFQ=$\frac{1}{2}$∠PFC,所以∠PFQ=∠CFQ=x.因为AB//CD,所以∠AEF+∠CFE=180°，所以75°+x+x+x=180°，所以x=35°,所以∠EFP=35°;
如图②,当点Q在CD的下方时，设∠CFQ=x,由∠CFQ=$\frac{1}{2}$∠PFC得∠PFC=2x,所以∠PFQ=3x,由折叠得∠PFE=∠PFQ=3x.因为AB//CD,所以∠AEF+∠CFE=180°，所以2x+3x+75°=180°，所以x=21°,所以∠EFP=3x=63°.综上所述，∠EFP的度数是35°或63°.

19. (6 分)计算:
(1)$-2^{2} - 3×(-1)^{3} + |-2|$;
(2)$(-2a^{2})^{3}·a^{6} - (-5a^{6})^{2}$.

答案：
(1)原式=−4−3×(−1)+2=−4+3+2=1.
(2)原式=−8$a^{6}$·$a^{6}$−25$a^{12}$=−8$a^{12}$−25$a^{12}$=−33$a^{12}$.

20. (4 分)先化简,再求值:$2(a^{2}b + ab^{2} - 1) - 2(a^{2}b - b) - 2ab^{2} + a$,其中$a = -1$,$b = 1014$.

答案： 原式=2$a^{2}$b+2ab²−2−2$a^{2}$b+2b−2ab²+a=2b+a−2.当a=−1,b=1014时，原式=2×1014+(−1)−2=2025.