《2025年学霸提优大试卷七年级数学上册苏科版》

9. 已知$y_{1} = x + 2,y_{2} = 4x - 7$,当$x = $5时,$y_{1} + y_{2} = 20$.

答案： 9.5　　[解析]$y_{1}+y_{2}=x+2+4x-7=20$,解得x=5.

10. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相遇? 译文:甲从长安出发,5天到齐国;乙从齐国出发,7天到长安.现乙先出发2天,甲才从长安出发.问多久后甲、乙相遇? 若设乙出发$x$天甲、乙相遇,则可列方程为$\frac{x}{7}+\frac{x-2}{5}=1$.

答案： 10.$\frac{x}{7}+\frac{x-2}{5}=1$　　[解析]由题可知,甲的速率为$\frac{1}{7}$,乙的速率为$\frac{1}{5}$,设乙出发x天,则甲出发(x−2)天,根据题意列方程为$\frac{x}{7}$+$\frac{x−2}{5}$=1.

11. 一个三角形的周长为81cm,三边长的比为$2:3:4$,则最长边比最短边长18cm.

答案： 11.18cm　　[解析]三角形三边长的比为2:3:4,分别设三角形的三边长为2xcm,3xcm,4xcm,所以2x+3x+4x=81,解得x=9,所以最长边为4×9=36(cm),最短边为2×9=18(cm),最长边比最短边长36−18=18(cm).

12. 数轴上表示数$2m$和$m + 2$的点到原点的距离相等,则$m$的值为2或$-\frac{2}{3}$.

答案： 12.2或$-\frac{2}{3}$　[解析]因为数轴上表示数2m和m+2的点到原点的距离相等,所以|2m|=|m+2|,即2m=m+2或2m=−(m+2).当2m=m+2时,解得m=2;当2m=−(m+2)时,解得m=$-\frac{2}{3}$.故答案为2或$-\frac{2}{3}$.

13. 一个两位数的十位数字与个位数字的和是9,把这个两位数加上27后,结果恰好成为数字对调后组成的两位数,则这个两位数是36.

答案： 13.36　[解析]根据题意，设十位数字为x,则个位数字为9−x，这个两位数为10x+9−x=9x+9,对调后的两位数为10(9−x)+x=90−9x,根据题意,得9x+9+27=90−9x,解得x=3,9−3=6,所以这个两位数为36.

14. (2025·南通期末)若关于$x的一元一次方程a(x - \frac{1}{2025}) + b = 2x + c - \frac{2}{2025}的解为x = 1$,则关于$y的一元一次方程ay + b = 2y + c的解为y = $____.

答案： 14.$\frac{2024}{2025}$　　[解析]a(x−$\frac{1}{2025}$)+b=2x+c−$\frac{2}{2025}$,a(x−$\frac{1}{2025}$)+b=2(x−$\frac{1}{2025}$)+c,观察可知关于y的一元一次方程ay+b=2y+c,形式与变形后的关于x的方程相似,令y=x−$\frac{1}{2025}$.因为关于x的一元一次方程a(x−$\frac{1}{2025}$)+b=2x+c−$\frac{2}{2025}$的解为x=1,所以关于y的一元一次方程ay+b=2y+c的解为y=x−$\frac{1}{2025}$=1−$\frac{1}{2025}$=$\frac{2024}{2025}$.

15. 如图,一个盛有水的圆柱形玻璃容器的内底面半径为8cm,容器内水的高度为18cm.如果把一根底面半径为4cm的实心玻璃棒垂直插人水中(水不会溢出),那么容器内的水将升高____6cm.

答案： 15.6cm　　[解析]设容器内的水将升高xcm,根据题意,得$\pi\cdot8^{2}×18+\pi\cdot4^{2}×(18+x)=\pi\cdot8^{2}×(18+x)$,解得x=6.故容器内的水将升高6cm.

16. 5个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实地告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数加起来除以2所得的数报出来.若报出来的数如图所示,则报5的人心里想的数是5.

答案： 16.5　　[解析]设报5的人心里想的数是x,根据报5和报3的人的数加起来除以2是4,得报3的人心里想的数是8−x;根据报3和报1的人的数加起来除以2是2,得报1的人心里想的数是2×2−(8−x)=x−4;根据报5和报2的人的数加起来除以2是1,得报2的人心里想的数是2×1−x=2−x;根据报2和报4的人的数加起来除以2是3,得报4的人心里想的数是3×2−(2−x)=x+4;根据报1和报4的人的数加起来除以2是5,得x−4+x+4=5×2,解得x=5,故报5的人心里想的数是5.

17. (2025·南京校级月考)如图,在长方形$ABCD$中,$AB = 8$厘米,$AD = 6$厘米,$P,Q$两动点同时出发,分别沿着长方形的边运动,$P点从B$点出发,顺时针旋转一圈,到达$B$点后停止运动,$Q点的运动路线为B→C→D$,$Q$点的运动速度分别为2厘米/秒,1厘米/秒,当一个动点到达终点时,另一个动点也同时停止运动.设两动点运动的时间为$t$秒,要使$\triangle BDP和\triangle ACQ$的面积相等,所有满足条件的$t$的值为____.

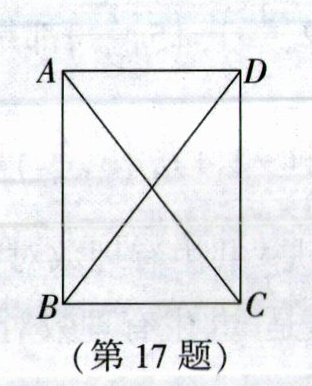
答案：
17.2.4或$\frac{74}{11}$或8或$\frac{130}{11}$　[解析]由题意进行分类讨论:
　　①当P点在AB上,Q点在BC上时(t≤4),如图①,
　　　　　　　　　　
BP=2t,CQ=6−t,因为△BDP与△ACQ的面积相等,所以$\frac{1}{2}$×6×2t=$\frac{1}{2}$×8×(6−t),解得t=2.4;
　　②当P点在AD上,Q点在BC上时(4＜t≤6),如图②，,
　　　　　　　　　　
DP=14−2t,CQ=6−t,要使△BDP与△ACQ的面积相等,则DP=CQ,即14−2t=6−t,解得t=8(舍去);
　　③当P点在AD上,Q点在CD上时(6＜t≤7),如图③,
　　　　　　　　　　
DP=14−2t,CQ=t−6,因为△BDP与△ACQ的面积相等,所以$\frac{1}{2}$×8×(14−2t)=$\frac{1}{2}$×6×(t−6),解得t=$\frac{74}{11}$;
　　④当P点在CD上,Q点在CD上时(7＜t≤11),如图④,
　　　　　　　　　　
DP=2t−14,CQ=t−6,要使△BDP与△ACQ的面积相等,则DP=CQ,即2t−14=t−6,解得t=8;
　　⑤当P点在BC上,Q点在CD上时(11＜t≤14),如图⑤,
　　　　　　　　　　
BP=28−2t,CQ=t−6,因为△BDP与△ACQ的面积相等,所以$\frac{1}{2}$×8×(28−2t)=$\frac{1}{2}$×6×(t−6),解得t=$\frac{130}{11}$.综上，满足条件的t的值为2.4或$\frac{74}{11}$或8或$\frac{130}{11}$.