《2025年学霸提优大试卷七年级数学上册苏科版》

1. (2024·河北中考)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图①所示的“表格算法”,图①表示$132×23$,运算结果为3036.图②表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图②中现有数据进行推断,正确的是 ( )


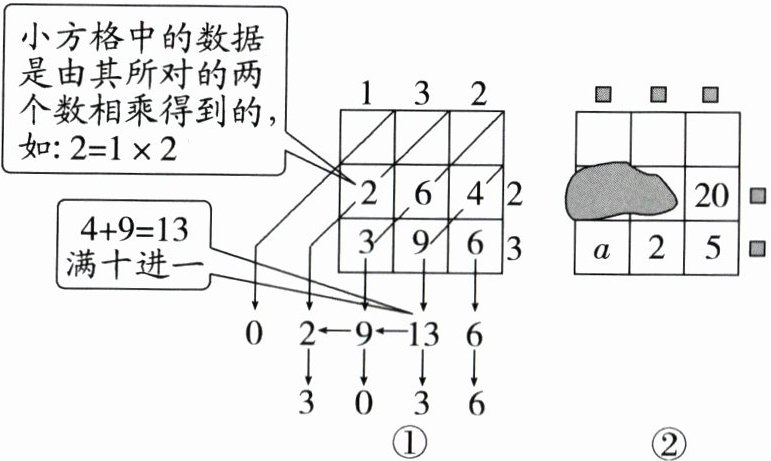
A.“20”左边的数是16
B.“20”右边的“■”表示5
C.运算结果小于6000
D.运算结果可以表示为$4100a + 1025$

答案：
D 【解析】设一个三位数与一个两位数分别为100x+10y+z和10m+n,如图①,则由题意得mz=20,nz=5,ny=2,nx=a,所以mz=4nz,即m=4n.因为ny=2,且n,y均为正整数,所以当n=2,y=1时,z=2.5不是正整数,不符合题意,故舍去;当n=1,y=2时,则m=4,z=5,x=a.如图②.A.“20”左边的数是2×4=8,故本选项不符合题意;B.“20”右边的“□”表示4,故本选项不符合题意;如图③,所以运算结果可以表示为1000(4a+1)+100a+20+5=4100a+1025,所以D选项符合题意,当a=2时,计算的结果大于6000,故C选项不符合题意.故选D.

2. (2024·烟台中考)《周髀算经》是中国现存最早的数理天文著作.书中记载这样一道题:“今有女子不善织,日减功迟.初日织五尺,末日织一尺,今三十日织讫.问织几何?”意思是:现有一个不擅长织布的女子,织布的速度越来越慢,并且每天减少的数量相同,第一天织了五尺布,最后一天仅织了一尺布,30天完工,问一共织了多少布? (C)
A.45尺
B.88尺
C.90尺
D.98尺

答案： C 【解析】设每天减少x尺布,因为第一天织了五尺布,最后一天仅织了一尺布,30天完工,所以5 - 29x = 1,解得x = $\frac{4}{29}$,所以5+(5 - $\frac{4}{29}$)+(5 - $\frac{8}{29}$)+…+1 = 90(尺),故选C.

3. 现代的数学符号体系,不仅使得数学语言变得简洁明了,还能更好地帮助人们总结出便于运算的各种运算法则,简明地揭示数量之间的相互关系.我国在1905年清朝学堂的课本中还用“$\frac {五}{丁}\frac {三}{丙}\frac {二七}{甲}\frac {}{乙}$”来表示相当于$\frac {d^{2}}{5}-\frac {c^{2}}{3}+\frac {a^{2}b^{2}}{27}$的代数式,观察其中的规律,“$\frac {五}{甲}\frac {三}{乙}\frac {甲}{丙}$”表示的代数式为 (C)
A.$\frac {5}{a^{2}}+\frac {3}{b^{2}}+\frac {a}{c^{2}}$
B.$\frac {5}{2a}+\frac {3}{b^{2}}-\frac {c^{2}}{a}$
C.$\frac {a^{2}}{5}+\frac {b^{2}}{3}-\frac {c^{2}}{a}$
D.$\frac {5}{2a}+\frac {3}{2b}-\frac {a}{2c}$

答案： C 【解析】根据给出的例题,列代数式即可.可知⊤表示“减号”,⊥表示“加号”;甲、乙、丙、丁分别对应a,b,c,d,且分子、分母需互换位置,由此可得“五⊥三甲甲≡乙≡⊤丙”表示的代数式为$\frac{a²}{5}$+$\frac{b²}{3}$-$\frac{c²}{a}$.故选C.

4. (2025·金水区模拟)汉代的《淮南万毕术》中记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法.为了探清一口深井的底部情况,如图,在井口放置一面平面镜可改变光路,当太阳光线AB与地面CD所成夹角$∠ABC = 50^{\circ}$时,已知$∠ABE = ∠FBM$,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需要调整平面镜EF与地面的夹角$∠EBC = $ (B)
A.$60^{\circ}$
B.$70^{\circ}$
C.$80^{\circ}$
D.$85^{\circ}$

答案： B 【解析】因为BM⊥CD,所以∠CBM = 90°.因为∠ABC = 50°,所以∠ABE + ∠FBM = 180° - 90° - 50° = 40°.因为∠ABE = ∠FBM,所以∠ABE = ∠FBM = 20°,所以∠EBC = 20° + 50° = 70°.故选B.