《2025年学霸提优大试卷七年级数学上册苏科版》

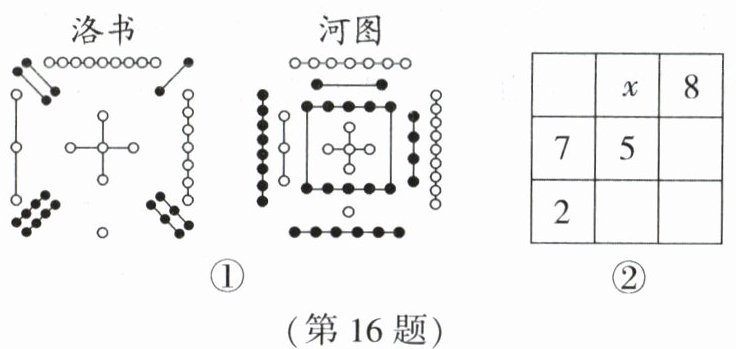
16. 新趋势数学文化如图①,河图洛书是中国古代流传下来的两幅神秘图案,被誉为“宇宙魔方”,是中华文化、阴阳五行术数之源.图②是由河图洛书得到的3×3的一个九宫格,把1~9这九个数填入方格中,使其行、列及对角线上的三个数之和都分别相等,则图②中x的值应为______.

1

答案： 1　　[解析]由题意可得$8 + x = 2 + 7$，所以$x = 1$.

17. 如图是某年9月的月历,中国烈士纪念日在9月份,小明用长方形按如图所示的方法从月历中任意框出3个数.若长方形框住的3个数的和为72,且中国烈士纪念日正好是这3个数中最大的数,则中国烈士纪念日的日期为9月30日.

答案： 30　　[解析]可以发现规律:这3个数的和是中间的数B的3倍.若长方形框住的3个数的和为72,则中间数B是$72÷3 = 24$，所以数C是30，所以中国烈士纪念日的日期为9月30日.

18. 新情境(2025·北京模拟)某校举办了“数学节”活动,其中有一项活动是“数学游戏挑战赛”,参赛学生要按顺序依次参加“九连环、七巧板、五子棋、二十四点、魔方、华容道、数独”七个项目(每个项目只能挑战一次).按照完成情况每个项目都分为参与奖、优秀奖、卓越奖,并奖励相应的积分.七个项目不同奖项对应的奖励积分如下表所示:

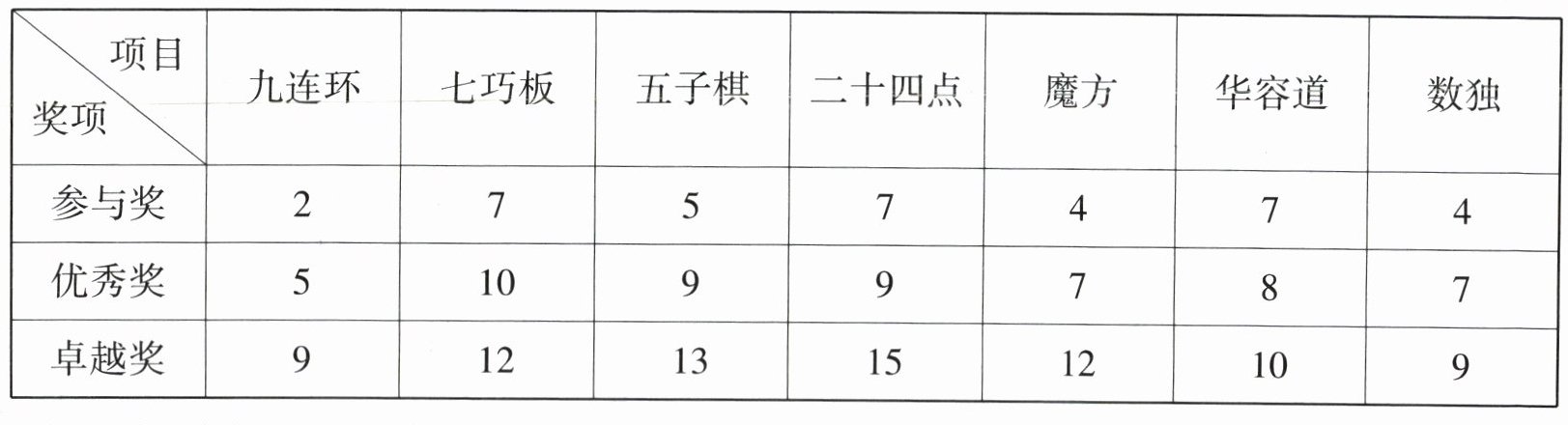
小明同学参加了此次“数学游戏挑战赛”活动,若知道小明在“九连环”项目中没有获得卓越奖,在“魔方”项目中获得了优秀奖,且在所有获得卓越奖项目的前一个项目中都获得参与奖,则可推断小明在“华容道”和“数独”这两个项目的积分之和最高为______,他参加此次“数学游戏挑战赛”活动的总积分最高为______.
[答案]：16　58

答案： 16　58　[解析]因为在所有获得卓越奖项目的前一个项目中都获得参与奖，所以当华容道和数独都获得优秀奖时，得分为$8 + 7 = 15$(分);当华容道获得参与奖、数独获得卓越奖时，得分为$7 + 9 = 16$(分)，所以可推断小明在“华容道”和“数独”这两个项目的积分之和最高为16分.因为小明在“九连环”项目中没有获得卓越奖，所以小明在“九连环”项目中可能获得参与奖或优秀奖.因为在所有获得卓越奖项目的前一个项目中都获得参与奖，所以:①当七巧板获得卓越奖时，九连环获得参与奖，其他三个项目获得优秀奖，所以总积分为$2 + 12 + 9 + 9 + 7 + 16 = 55$(分);②当七巧板、二十四点获得卓越奖时，九连环、五子棋获得参与奖，所以总积分为$2 + 12 + 5 + 15 + 7 + 16 = 57$(分);③当五子棋获得卓越奖，二十四点获得优秀奖，九连环获得优秀奖时，七巧板获得参与奖，所以总积分为$5 + 7 + 13 + 9 + 7 + 16 = 57$(分);④当二十四点获得卓越奖，九连环、七巧板获得优秀奖时，五子棋获得参与奖，总积分为$5 + 10 + 5 + 15 + 7 + 16 = 58$(分).综上所述，他参加此次“数学游戏挑战赛”活动的总积分最高为58分.

19. (8分)如图是某商品包装盒上的一个标签,你能从这个标签上看出这个商品的包装盒有多重、体积有多大吗?

答案： 包装盒重:$6.0 - 5.5 = 0.5$(kg)，体积:$70×60×150 = 630000$($\text{cm}^3$).答:包装盒重0.5kg，体积为630000$\text{cm}^3$.