第155页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
19. 如图,A,B,C为数轴上的点,$AC = 4$,点B为AC的中点,点P为数轴上的任意一点,则$PA+PB + 2PC$的最小值为______.
]

]

答案:
6 【解析】因为AC = 4,点B为AC的中点,所以AB = BC = 2.当点P位于点A左侧时,如图①所示
PA+PB+2PC = PA+PA+AB+2(PA+AC)=4PA + 10;
当点P与点A重合时,如图②所示

PA+PB+2PC = 0 + 2 + 8 = 10;
当点P位于点A与点B之间时,如图③所示

PA+PB+2PC = 2 + 2(PB+BC)=2PB + 6;
当点P与点B重合时,如图④所示

PA+PB+2PC = 2 + 0 + 2×2 = 6;
当点P位于点B与点C之间时,如图⑤所示

PA+PB+2PC = AB+PB+PB+2PC = 2 + 4 = 6;
当点P与点C重合时,如图⑥所示

PA+PB+2PC = 4 + 2 = 6;
当点P位于点C右侧时,如图所示

PA+PB+2PC = AC+PC+BC+PC+2PC = 6 + PC.
综上,PA+PB+2PC的最小值为6.
6 【解析】因为AC = 4,点B为AC的中点,所以AB = BC = 2.当点P位于点A左侧时,如图①所示
PA+PB+2PC = PA+PA+AB+2(PA+AC)=4PA + 10;
当点P与点A重合时,如图②所示

PA+PB+2PC = 0 + 2 + 8 = 10;
当点P位于点A与点B之间时,如图③所示

PA+PB+2PC = 2 + 2(PB+BC)=2PB + 6;
当点P与点B重合时,如图④所示

PA+PB+2PC = 2 + 0 + 2×2 = 6;
当点P位于点B与点C之间时,如图⑤所示

PA+PB+2PC = AB+PB+PB+2PC = 2 + 4 = 6;
当点P与点C重合时,如图⑥所示

PA+PB+2PC = 4 + 2 = 6;
当点P位于点C右侧时,如图所示

PA+PB+2PC = AC+PC+BC+PC+2PC = 6 + PC.
综上,PA+PB+2PC的最小值为6.
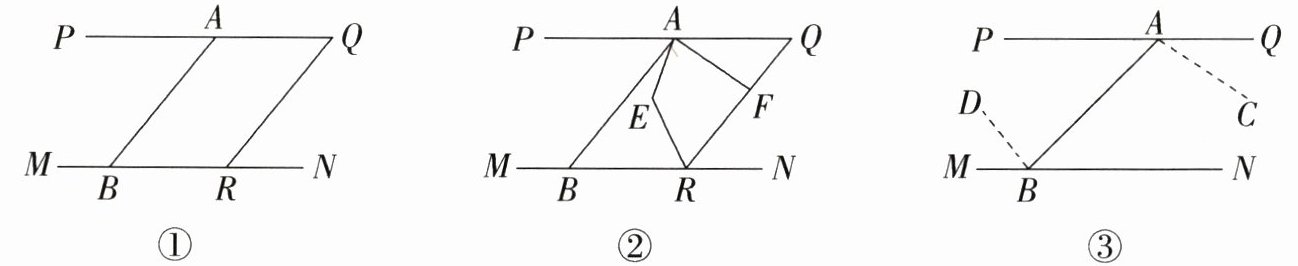
20. (2024·扬州期末)已知:如图,$PQ// MN$,点B为MN上一点,$∠ABN = ∠Q$.
(1)如图①,试说明:$AB// QR$;
(2)如图②,点F为线段QR上一点,$∠PAF的平分线与∠BRF$的平分线相交于点E,请写出$∠AER与∠AFR$的数量关系,并说明理由;
(3)中欧班列是高质量共建“一带一路”的互联互通大动脉,中欧班列为了安全起见在某段铁路两旁安置了A,B两座可旋转探照灯.如图③,假定主道路是平行的,即$PQ// MN$,连接AB,且$∠ABN = 45^{\circ}$.灯A发出的射线AC自AQ顺时针旋转至AP,灯B发出的射线BD自BM顺时针旋转至BN后便立即回转,当射线BD回转至BM后两条射线停止运动,两灯不停交叉照射巡视.灯A转动的速度是2度/秒,灯B转动的速度是8度/秒.若它们同时开始转动,设转动时间为t秒,当AC与BD互相垂直时,请直接写出此时t的值.
]
(1)如图①,试说明:$AB// QR$;
(2)如图②,点F为线段QR上一点,$∠PAF的平分线与∠BRF$的平分线相交于点E,请写出$∠AER与∠AFR$的数量关系,并说明理由;
(3)中欧班列是高质量共建“一带一路”的互联互通大动脉,中欧班列为了安全起见在某段铁路两旁安置了A,B两座可旋转探照灯.如图③,假定主道路是平行的,即$PQ// MN$,连接AB,且$∠ABN = 45^{\circ}$.灯A发出的射线AC自AQ顺时针旋转至AP,灯B发出的射线BD自BM顺时针旋转至BN后便立即回转,当射线BD回转至BM后两条射线停止运动,两灯不停交叉照射巡视.灯A转动的速度是2度/秒,灯B转动的速度是8度/秒.若它们同时开始转动,设转动时间为t秒,当AC与BD互相垂直时,请直接写出此时t的值.
]

答案:
(1)因为PQ//MN,所以∠BAQ + ∠ABN = 180°.因为∠ABN = ∠Q,所以∠BAQ + ∠Q = 180°,所以AB//QR.
(2)∠AFR + 2∠AER = 360°.理由如下:如图①,延长AE交MN于点G,延长AF交MN于点H.因为AE平分∠PAF,RE平分∠BRF,所以设∠PAE = ∠EAF = α,∠ERB = ∠ERF = β.因为PQ//MN,所以∠EGR = ∠PAE = α,所以∠AER = 180° - ∠GER = ∠EGR + ∠ERB = α + β.同理∠AFR = 180° - ∠RFH = ∠QRH + ∠AHR = ∠QRH + ∠QAF = 180° - 2β + 180° - 2α = 360° - 2(α + β).所以∠AFR + 2∠AER = 360°.

(3)t = 15或27或45. 【解析】射线AC运动时间为180÷2 = 90(秒),射线BD的运动时间为360÷8 = 45(秒),所以射线AC最多运动到AC⊥PQ.因为PQ//MN,所以∠QAT = ∠ATB = (2t)°,
① 如图②,当BD,AC未相遇时,设射线AC交MN于点T,射线BD交PQ于点S,因为AC与BD互相垂直,所以∠SBT + ∠ATB = 90°,所以180 - 8t + 2t = 90,解得t = 15;
② 如图③,当BD返回时,∠DBT + ∠ATB = 90°,所以8t - 180 + 2t = 90,解得t = 27;
③ 当BD回到BM时,AC刚好垂直PQ,所以t = 45.
综上所述,$t_{1} = 15$,$t_{2} = 27$,$t_{3} = 45$时,AC与BD互相垂直.

(1)因为PQ//MN,所以∠BAQ + ∠ABN = 180°.因为∠ABN = ∠Q,所以∠BAQ + ∠Q = 180°,所以AB//QR.
(2)∠AFR + 2∠AER = 360°.理由如下:如图①,延长AE交MN于点G,延长AF交MN于点H.因为AE平分∠PAF,RE平分∠BRF,所以设∠PAE = ∠EAF = α,∠ERB = ∠ERF = β.因为PQ//MN,所以∠EGR = ∠PAE = α,所以∠AER = 180° - ∠GER = ∠EGR + ∠ERB = α + β.同理∠AFR = 180° - ∠RFH = ∠QRH + ∠AHR = ∠QRH + ∠QAF = 180° - 2β + 180° - 2α = 360° - 2(α + β).所以∠AFR + 2∠AER = 360°.

(3)t = 15或27或45. 【解析】射线AC运动时间为180÷2 = 90(秒),射线BD的运动时间为360÷8 = 45(秒),所以射线AC最多运动到AC⊥PQ.因为PQ//MN,所以∠QAT = ∠ATB = (2t)°,
① 如图②,当BD,AC未相遇时,设射线AC交MN于点T,射线BD交PQ于点S,因为AC与BD互相垂直,所以∠SBT + ∠ATB = 90°,所以180 - 8t + 2t = 90,解得t = 15;
② 如图③,当BD返回时,∠DBT + ∠ATB = 90°,所以8t - 180 + 2t = 90,解得t = 27;
③ 当BD回到BM时,AC刚好垂直PQ,所以t = 45.
综上所述,$t_{1} = 15$,$t_{2} = 27$,$t_{3} = 45$时,AC与BD互相垂直.

21. 某数学兴趣小组进行课题学习:用长方形硬纸板制作长方体纸盒.
材料:长方形硬纸板ABCD,AD长为15,AB长为3.
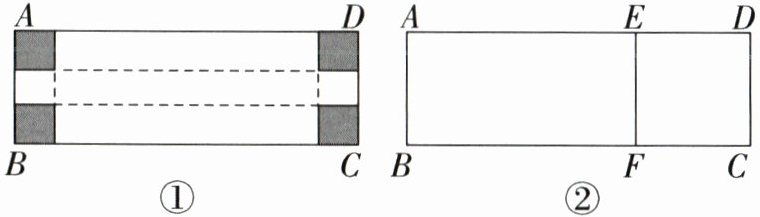
(1)初步感受:如图①,在长方形硬纸板四个角上剪去四个边长为1的小正方形,将剩下的硬纸板折叠成无盖的长方体纸盒,则该长方体纸盒底面周长为______.
(2)深入探究:兴趣小组为了充分利用硬纸板(硬纸板无剩余),采用新的裁剪方法:如图②所示,用EF把长方形ABCD分成2个长方形,将长方形ABFE折叠成纸盒的侧面,将长方形CDEF做纸盒的下底面,做成一个无盖的长方体纸盒,请你求这个纸盒底面的边长.
(3)问题解决:在以上操作的启发之下,你能充分利用该长方形硬纸板(硬纸板无剩余),制作一个有盖的长方体纸盒吗?若能,请画出两种裁剪设计图并求出所做纸盒的底面边长,若不能,请说明理由.
]
材料:长方形硬纸板ABCD,AD长为15,AB长为3.

(1)初步感受:如图①,在长方形硬纸板四个角上剪去四个边长为1的小正方形,将剩下的硬纸板折叠成无盖的长方体纸盒,则该长方体纸盒底面周长为______.
(2)深入探究:兴趣小组为了充分利用硬纸板(硬纸板无剩余),采用新的裁剪方法:如图②所示,用EF把长方形ABCD分成2个长方形,将长方形ABFE折叠成纸盒的侧面,将长方形CDEF做纸盒的下底面,做成一个无盖的长方体纸盒,请你求这个纸盒底面的边长.
(3)问题解决:在以上操作的启发之下,你能充分利用该长方形硬纸板(硬纸板无剩余),制作一个有盖的长方体纸盒吗?若能,请画出两种裁剪设计图并求出所做纸盒的底面边长,若不能,请说明理由.
]
答案:
(1) 28 【解析】如图①,因为AD = BC = 15,AB = CD = 3,所以GJ = HI = 15 - 2 = 13,GH = IJ = 3 - 2 = 1,所以底面周长为GJ + HI + GH + IJ = 28.

(2) 设DE = CF = x,则长方体纸盒的底面周长为EF + CD + DE + CF = 2x + 6.由长方形ABFE折叠成纸盒的侧面,得AE的长度为底面周长的长度,则AE = 2x + 6.因为AD = 15,所以AE + DE = 15,即2x + 6 + x = 15,解得x = 3.此时四边形CDEF为正方形,即这个纸盒底面的边长为3.
(3) 能制作一个有盖的长方体纸盒.理由如下:
方案1: 将长方形DCFE,EFNM作为长方体纸盒的上、下底面,长方形ABNM作为长方体纸盒的侧面,如图②所示,

设ME = ED = NF = CF = a,则长方体纸盒的底面周长为ME + MN + NF + EF = 2a + 6,由长方形ABNM作为长方体纸盒的侧面,得AM的长度为底面周长的长度,则AM = 2a + 6.因为AD = 15,所以AM + ME + DE = 15,即2a + 6 + a + a = 15,解得$a=\frac{9}{4}$,所以所做纸盒的底面相邻两边一边为3,一边为$\frac{9}{4}$.
方案2: EF将长方形ABCD分成两个长方形,则EF = 3.分别取EF,CD的中点G,H,连接GH,则$EG = GF=\frac{1}{2}EF=\frac{1}{2}CD=\frac{3}{2}$.设DE = y,则AE = 15 - y,由题意,得$2(y+\frac{3}{2})=15 - y$,解得y = 4,所以所做纸盒的底面相邻两边长一边为4,一边为$\frac{3}{2}$.

(1) 28 【解析】如图①,因为AD = BC = 15,AB = CD = 3,所以GJ = HI = 15 - 2 = 13,GH = IJ = 3 - 2 = 1,所以底面周长为GJ + HI + GH + IJ = 28.

(2) 设DE = CF = x,则长方体纸盒的底面周长为EF + CD + DE + CF = 2x + 6.由长方形ABFE折叠成纸盒的侧面,得AE的长度为底面周长的长度,则AE = 2x + 6.因为AD = 15,所以AE + DE = 15,即2x + 6 + x = 15,解得x = 3.此时四边形CDEF为正方形,即这个纸盒底面的边长为3.
(3) 能制作一个有盖的长方体纸盒.理由如下:
方案1: 将长方形DCFE,EFNM作为长方体纸盒的上、下底面,长方形ABNM作为长方体纸盒的侧面,如图②所示,

设ME = ED = NF = CF = a,则长方体纸盒的底面周长为ME + MN + NF + EF = 2a + 6,由长方形ABNM作为长方体纸盒的侧面,得AM的长度为底面周长的长度,则AM = 2a + 6.因为AD = 15,所以AM + ME + DE = 15,即2a + 6 + a + a = 15,解得$a=\frac{9}{4}$,所以所做纸盒的底面相邻两边一边为3,一边为$\frac{9}{4}$.
方案2: EF将长方形ABCD分成两个长方形,则EF = 3.分别取EF,CD的中点G,H,连接GH,则$EG = GF=\frac{1}{2}EF=\frac{1}{2}CD=\frac{3}{2}$.设DE = y,则AE = 15 - y,由题意,得$2(y+\frac{3}{2})=15 - y$,解得y = 4,所以所做纸盒的底面相邻两边长一边为4,一边为$\frac{3}{2}$.

查看更多完整答案,请扫码查看


