《2025年学霸提优大试卷七年级数学上册苏科版》

7. 如图,点M在线段AN的延长线上,且线段$MN = 10$,第一次操作：分别取线段AM和AN的中点$M_{1}$,$N_{1}$；第二次操作：分别取线段$AM_{1}和AN_{1}的中点M_{2}$,$N_{2}$；第三次操作：分别取线段$AM_{2}和AN_{2}的中点M_{3}$,$N_{3}$；…连续这样操作2025次,则每次的两个中点所形成的所有线段之和$M_{1}N_{1}+M_{2}N_{2}+…+M_{2025}N_{2025}= $C
A.$10+\frac{5}{2^{2024}}$
B.$10+\frac{5}{2^{2025}}$
C.$10-\frac{5}{2^{2024}}$
D.$10-\frac{5}{2^{2025}}$
]

答案： C 【解析】因为MN = 10,$M_{1},N_{1}$分别为AM,AN的中点,所以$M_{1}N_{1}=AM_{1}-AN_{1}=\frac{1}{2}AM-\frac{1}{2}AN=\frac{1}{2}(AM - AN)=\frac{1}{2}MN=\frac{1}{2}×10 = 5$.因为$M_{2},N_{2}$分别为$AM_{1},AN_{1}$的中点,所以$M_{2}N_{2}=AM_{2}-AN_{2}=\frac{1}{2}AM_{1}-\frac{1}{2}AN_{1}=\frac{1}{2}(AM_{1}-AN_{1})=\frac{1}{2}M_{1}N_{1}=\frac{1}{2}×5=\frac{5}{2}$.因为$M_{3},N_{3}$分别为$AM_{2},AN_{2}$的中点,所以$M_{3}N_{3}=AM_{3}-AN_{3}=\frac{1}{2}AM_{2}-\frac{1}{2}AN_{2}=\frac{1}{2}(AM_{2}-AN_{2})=\frac{1}{2}M_{2}N_{2}=\frac{1}{2}×\frac{5}{2}=\frac{5}{2^{2}}$,…,由此可得$M_{n}N_{n}=\frac{5}{2^{n - 1}}$,所以$M_{1}N_{1}+M_{2}N_{2}+\dots+M_{2025}N_{2025}=5+\frac{5}{2}+\frac{5}{2^{2}}+\dots+\frac{5}{2^{2024}}=10×(\frac{1}{2}+\frac{1}{2^{2}}+\dots+\frac{1}{2^{2025}})=10×(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\dots+\frac{1}{2^{2024}}-\frac{1}{2^{2025}})=10×(1-\frac{1}{2^{2025}})=10-\frac{5}{2^{2024}}$.故选C.

8. (2024·攀枝花中考)如图是由棱长为1的小正方体堆积成的图形.若按照这样的规律继续摆放,则第8层需要摆放36块小正方体.

答案： 36 【解析】第一层:1块;第二层:(1 + 2)块;第三层:(1 + 2 + 3)块;…;第n层:$1 + 2 + 3 + \dots + n = [\frac{1}{2}n(n + 1)]$块.当n = 8时,$\frac{1}{2}×8×9 = 36$(块).

9. (2024·潍坊中考)将连续的正整数排成如图所示的数表.记$a_{(i,j)}$为数表中第i行第j列位置的数,如$a_{(1,2)} = 4$,$a_{(3,2)} = 8$,$a_{(5,4)} = 22$.若$a_{(m,n)} = 2024$,则$m = $45,$n = $2.

答案： 45 2 【解析】由题图中排布可知,当正整数为$k^{2}$时,若k为奇数,则$k^{2}$在第k行,第1列,下一个数在下一行,上一个数在第2列;若k为偶数,则$k^{2}$在第1行,第k列,下一个数在下一列,上一个数在第2行;因为$a_{(m,n)} = 2024 = 2025 - 1 = 45^{2} - 1$,而2025 = $45^{2}$,在第45行,第1列,所以2024在第45行,第2列,所以m = 45,n = 2.

10. (2024·西安校级期中)我国宋朝时期的数学家杨辉,曾将大小完全相同的圆弹珠逐层堆积,形成“三角垛”.如图,图①有1颗弹珠,图②有3颗弹珠,图③有6颗弹珠,往下依次是图④,图⑤,…,若用$a_{n}$表示图n的弹珠数,其中$n = 1$,2,3,…,则$\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+…+\frac{1}{a_{2025}}$的值是______$\frac{2025}{1013}$.

答案： $\frac{2025}{1013}$ 【解析】观察题图的变化可知,题图①有1颗弹珠,即1 = 1;题图②有3颗弹珠,即1 + 2 = 3;题图③有6颗弹珠,即1 + 2 + 3 = 6;题图④有10颗弹珠,即1 + 2 + 3 + 4 = 10,…,所以题图ⓝ的弹珠数为$1 + 2 + 3 + \dots + n = \frac{n(n + 1)}{2}$,所以$a_{n}=\frac{n(n + 1)}{2}$,则$\frac{1}{a_{n}}=\frac{2}{n(n + 1)}=2(\frac{1}{n}-\frac{1}{n + 1})$.所以$\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+\dots+\frac{1}{a_{2025}}=2×(1 - \frac{1}{2})+2×(\frac{1}{2}-\frac{1}{3})+2×(\frac{1}{3}-\frac{1}{4})+\dots+2×(\frac{1}{2025}-\frac{1}{2026})=2×(1-\frac{1}{2026})=2×\frac{2025}{2026}=\frac{2025}{1013}$.

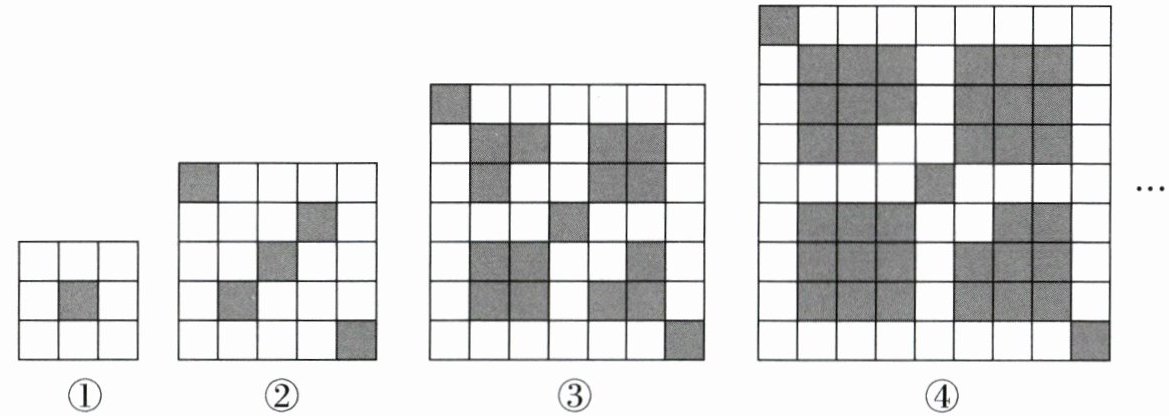
11. (2025·合肥模拟)某数学活动小组用大小一样的灰白两种颜色的小正方形纸片,按如图的规律摆放.请根据图中的信息解决下列问题.
(1)图⑤中共有65个灰色小正方形,图n(n为正整数)中共有4(n - 1)^{2}+1个灰色小正方形.
(2)若某个图形中共有116个白色小正方形,则该图形中共有多少个灰色小正方形？
]

由题知,题图①中白色小正方形的个数为8 = 12×1 - 4;题图②中白色小正方形的个数为20 = 12×2 - 4;题图③中白色小正方形的值为32 = 12×3 - 4;…,所以题图ⓝ中白色小正方形的个数为(12n - 4),当12n - 4 = 116时,解得n = 10,则4(n - 1)^{2}+1 = 4×(10 - 1)^{2}+1 = 325(个),所以该图形中共有325个灰色小正方形.

答案：
(1) 65 [4(n - 1)^{2}+1] 【解析】由题中所给图形可知,题图①中灰色小正方形的个数为1 = 4×0^{2}+1;题图②中灰色小正方形的个数为5 = 4×1^{2}+1;题图③中灰色小正方形的个数为17 = 4×2^{2}+1;…,所以题图ⓝ中灰色小正方形的个数为[4(n - 1)^{2}+1].当n = 5时,4(n - 1)^{2}+1 = 4×(5 - 1)^{2}+1 = 65,即题图⑤中灰色小正方形的个数为65.
(2) 由题知,题图①中白色小正方形的个数为8 = 12×1 - 4;题图②中白色小正方形的个数为20 = 12×2 - 4;题图③中白色小正方形的值为32 = 12×3 - 4;…,所以题图ⓝ中白色小正方形的个数为(12n - 4),当12n - 4 = 116时,解得n = 10,则4(n - 1)^{2}+1 = 4×(10 - 1)^{2}+1 = 325(个),所以该图形中共有325个灰色小正方形.